Conduttori, Semiconduttori, isolanti
Conduttori sono quei materiali che fanno passare la corrente elettrica;
isolanti quei materiali che non fanno passare la corrente elettrica;
Semiconduttori quei materiali che hanno caratteristiche comprese fra quelle dei conduttori e degli isolanti e che in determinate condizioni possono condurre l’elettricità.
Possiamo anche affermare che , relativamente alla loro resistività , i conduttori hanno, come ordine di grandezza,
ρ = 10-3 Ωcm , gli isolanti hanno ρ = 105 Ωcm , i semiconduttori hanno ρ compresa fra 10-3 e 105 Ωcm.
Per avere un ‘idea della differenza fra questi tre tipi di materiali , possiamo fare qualche considerazione relativamente alla loro struttura atomica e dire, in modo molto ma molto ma molto semplicistico, che gli elettroni degli atomi di cui sono costituiti ruotano su orbite aventi ben stabiliti livelli energetici . Gli elettroni dell’orbita esterna costituiscono gli elettroni di valenza; se a questi ultimi forniamo una determinata energia essi possono passare in una banda avente energia superiore (banda di conduzione), dove possono essere utilizzati per la conduzione elettrica.
Per i materiali conduttori questa energia è minima , anzi la banda di energia dell’orbita esterna si sovrappone a quella dell’orbita di conduzione ; è come se esistesse nel materiale conduttore una nube di elettroni sempre disponibili per la conduzione . Per i materiali isolanti esiste una banda proibita, che separa la banda di valenza da quella di conduzione, per superare la quale occorre fornire una notevole energia ; è quindi quasi impossibile che elettroni disponibili per la conduzione si trovino nella banda di conduzione.
Per quanto riguarda i semiconduttori questa banda proibita è molto più piccola di quella degli isolanti e fornendo una determinata quantità di energia è possibile portare degli elettroni dalla banda di valenza a quella di conduzione. (vedi fig.1)
CONDUTTORI METALLICI

I metalli sono dei solidi cristallini che hanno elettroni di valenza liberi di muoversi.
Gli atomi che costituiscono il reticolo cristallino perdono un elettrone diventano ioni positivi e, a temperatura superiore a 0 K, non possono far altro che oscillare.
gli elettroni liberati, a temperature superiori a 0 K possono muoversi caoticamente all' interno del reticolo.
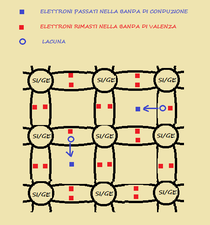
in fig.1a è rappresentato in modo bidimensionale un reticolo cristallino, (nella realtà è evidente che il reticolo è tridimensionale e assume diverse forme a seconda del metallo) in verde sono rappresentati gli ioni fissi; i cerchietti rossi col segno meno sono gli elettroni che costituiscono il gas elettronico.
In conclusione a temperatura pari a 0 K nulla si muove , a temperatura superiore si formano gli ioni positivi che rimangono fissi e possono solo oscillare intorno alla loro posizione e si liberano gli elettroni che si muovono in modo caotico all'interno del cristallo. In mancanza di campo elettrico la loro posizione mediamente non cambia e quindi la velocità di deriva è pari a zero.
cos'è la velocità di deriva Vd ?
Per capirlo vediamo di disegnare il grafico di fig. 1b che rappresenta la variazione della posizione dell'elettrone libero in funzione del tempo.
Velocità di deriva nei metalli

Supponiamo di avere il campo elettrico pari a Zero, in questa condizione l'elettrone non è soggetto ad alcuna forza e si muove di moto rettilineo uniforme e procede a zig zag come indicato dalla spezzata rossa di fig.1b, ad ogni urto o con altri elettroni o con gli ioni che oscillano cambiano direzione e dopo un certo periodo Δt ci accorgiamo che mediamente l'elettrone non si è spostato dalla sua posizione iniziale
Se ora introduciamo un campo elettrico E [V/m]. per esempio maggiore di zero l'elettrone sarà soggetto alla forza F = -q E .
Questa forza costante farà muovere l'elettrone con un moto uniformemente accelerato ed il suo andamento sarà quello della spezzata verde di fig.1b
Se facciamo la media di questi spostamenti ci accorgiamo che nel periodo Δt mediamente lo spostamento dell'elettrone sarà pari a Δx che assume il nome di deriva.
Se ora calcoliamo la variazione della deriva nel tempo Δt otteniamo la velocità di deriva Vd dell'elettrone ; trattasi evidentemente di una velocità media.
Si conclude che quando E = 0 non si ha deriva e quindi velocità di deriva e quando il campo è diverso da zero si ha deriva e velocità di deriva .
La velocità di deriva è proporzionale al campo elettrico ; nel caso del campo elettrico E>0 si ha Vd = - μE ; la Vd è espressa in [m/s] .
il coefficiente di proporzionalità μ rappresenta la mobilità dell'elettrone. ed è espresso in [m2/Vs].
Nella fig.1b è rappresentata in azzurro l'andamento della velocità istantanea dell'elettrone.
il primo tratto ha una pendenza negativa che rappresenta l'accelerazione a =-qE/m ( m è la massa dell'elettrone) che risulta negativa in quanto risulta E>0 e la carica dell'elettrone è negativa.
Dopo il primo urto si ha una riduzione della velocità ed una accelerazione negativa uguale alla precedente che la riduce ulteriormente, dopo il secondo urto si ha un'altra discontinuità ed un aumento della velocità che poi viene ridotta dalla accelerazione negativa ...e così di seguito.
Se dopo l'intervallo Δt faccio la media delle velocità istantanee ottengo la velocità di deriva Vd.
Nella fig.1c si dimostra come partendo da alcune considerazioni sulla velocità di deriva si arrivi alle due leggi di Ohm.
SEMICONDUTTORI INTRINSECI
Fra i semiconduttori più utilizzati in elettronica citiamo il Germanio ed il Silicio che hanno entrambi quattro elettroni nella banda di valenza.
Questi materiali si presentano come cristalli che schematicamente possono essere rappresentati come in fig.2.
A temperatura superiore allo zero assoluto esiste una probabilità non nulla che un elettrone del cristallo acquisisca energia sufficiente a fargli superare la banda proibita e a portarlo nella banda di conduzione ; in tal modo l’elettrone abbandona il suo atomo , che diventa uno ione positivo, e si lascia dietro un legame incompleto detto lacuna.
Gli elettroni che passano nella banda di conduzione si chiamano portatori N (negativi) e le lacune portatori P (positivi).
In un semiconduttore intrinseco il numero dei portatori P è uguale a quello dei portatori N; cioè:
N = P = Ni .
Ni dipende dalla temperatura infatti si ha :
Ni = KT2/3 e (-Eg/KT)
Eg e K sono costanti che dipendono dal materiale
A temperatura ambiente 20, 25 °C un semiconduttore intrinseco ( non drogato) ha nella sua banda di conduzione un numero di elettroni che si aggira sui 1010 elettroni/cm3 cioè un elettrone ogni 1012 atomi; infatti in un cristallo sono presenti circa 1022 atomi/cm3.
Si può far aumentare la capacità di conduzione dei semiconduttori, drogandoli.
Velocità di deriva nei semiconduttori intrinseci

Schematizziamo sul piano (fig. 2a) dei cristalli di semiconduttore (silicio o germanio).
A temperatura superiore allo zero assoluto qualche elettrone si libera e si rende disponibile per la conduzione.
Se applico un campo elettrico E gli elettroni liberi si muovono in direzione opposta al campo (vedi elettrone 1 di fig.2a) e nasce una corrente In che ha la stessa direzione del campo.
la lacuna lasciata libera dall'elettrone 1 può essere occupata dall'elettrone 2 (elettrone di valenza) , dico può essere perché l'elettrone 2 può :
- avere tanta energia da rendersi disponibile per la conduzione e quindi liberarsi e concorrere alla corrente In;
- può non avere energia sufficiente a spostarsi e rimanere dove si trova;
- può avere energia sufficiente per fare un salto ed andare ad occupare la vicina lacuna lasciata libera dall'elettrone 1 .
Supponiamo che l'elettrone 2 si trovi nell'ultima situazione, in questa situazione lascia il suo posto libero e va ad occupare il posto 1 , va cioè a formare la lacuna 2 che può essere occupata dall'elettrone 3............... proseguendo il ragionamento ci rendiamo conto che la lacuna si sposta nella direzione del campo e concorre a formare la corrente Ip ..
La lacuna col suo spostamento non è qualcosa di reale ma è considerata tale e viene chiamata "quasi particella" . essa rappresenta il moto collettivo degli elettroni di valenza ed il suo studio diventa più semplice e comprensibile del complesso moto collettivo degli elettroni di valenza.
Gli elettroni che col loro spostamento determinano il nascere delle lacune sono elettroni di valenza che non concorrono alla formazione della corrente In .
Le due correnti In e Ip sono correnti di deriva
Per quanto riguarda la velocità di deriva vale quanto detto per i metalli; cioè:
- Vn = - μn E ; μn è la mobilità dell'elettrone;
- Vp = μpE ; μp è la mobilità della lacuna.

Per quanto riguarda la corrente di deriva possiamo dire che è data dalla somma della corrente di deriva degli elettroni e della corrente di deriva delle lacune.
Vediamo perché.
Prendiamo in considerazione il cilindro di semiconduttore di fig.2a e poniamoci due domande; la prima:
- Quanti elettroni Δn passano nel tempo Δt attraverso la sez. A ?
Evidentemente passano tutti gli elettroni che si trovano nel cilindro avente il volume pari a : Vdn Δt A
il numero di elettroni passanti sarà pari ad n che rappresenta il numero di elettroni per unità di volume , per il volume Vdn Δt A.
Quindi sarà Δn = n Vdn Δt A.
la carica è Δq = -q Δn = -q n Vdn Δt A.
la corrente è
In= Δq/Δt = -q n Vdn A. = q n A μn E;
la seconda domanda è:
- Quante lacune Δp (quasi particelle) passano nel tempo Δt attraverso la sez. A ?
Evidentemente passano tutte le lacune che si trovano nel cilindro avente il volume pari a : Vdp Δt A
il numero di lacune passanti sarà pari ad p che rappresenta il numero di lacune per unità di volume , per il volume Vdp Δt A.
Quindi sarà Δn = p Vd Δt A.
la carica è Δq = q Δp = q p Vdp Δt A.
la corrente è
Ip= Δq/Δt = q p Vdp A. = q p A μp E;
la corrente totale di deriva sarà la somma
In + Ip .= qAE (nμn+ pμp)
Velocità di diffusione

La corrente di diffusione si ha nei semiconduttori anche quando il campo elettrico è nullo (E=0); perché si manifesti questa corrente occorre che la concentrazione degli elettroni e/o delle lacune non sia uniforme..
Prendiamo in considerazione la fig.2c .
Vediamo che la concentrazione degli elettroni e delle lacune varia con x .
Poiché in assenza di campo il movimento degli elettroni e delle lacune è caotico avremo che alcune lacune ed alcuni elettroni si sposteranno verso destra ed altre lacune ed altri elettroni verso sinistra.
Ci aspettiamo però, poiché la concentrazione degli elettroni e delle lacune diminuisce verso le x crescenti, che sia gli elettroni che le lacune abbiano uno spostamento netto verso le x crescenti
La direzione della corrente allora dipende dalla derivata (pendenza della retta verde) che nel caso in figura è negativa.
Possiamo allora scrivere :
- Per gli elettroni:
In = ( -q) Dn (-dn/dx) A = q Dn dn/dx A
- Per le lacune:
Ip = ( +q) Dp (-dp/dx) A = - q Dp dp/dx A
In queste espressioni Dn è la costante di diffusione o diffusività degli elettroni e Dp è la costante di diffusione o diffusività delle lacune.
La corrente totale è data dalla somma della corrente di deriva e della corrente di diffusione secondo il modello "drift diffusion" (DD), in italiano "Modello di deriva e diffusione"
La corrente totale vale:
I = In + Ip = q μnnEA + q Dn dn/dx A + q μppEA - q Dp dp/dx
EINSTEIN ha trovato una relazione che lega la mobilità μ alla diffusività D;
per gli elettroni la relazione è : Dn = ( KT /q ) μn
per le lacune la relazione è : Dp = ( KT /q ) μp
K è la costante di Boltzmann.
SEMICONDUTTORI ESTRINSECI O DROGATI
Se si aggiunge al cristallo una piccola percentuale di atomi di altri elementi si hanno forti cambiamenti nelle proprietà elettriche del cristallo che viene detto "DROGATO".
Gli elementi che posso aggiungere possono essere trivalenti (hanno tre elettroni nella banda di valenza) o pentaventi (hanno 5 elettroni nella banda di valenza).
Se aggiungo al cristallo un elemento trivalente è come se aggiungessi una lacuna; in tal caso il drogaggio e di tipo P e l'atomo aggiunto si chiama accettore.
Se aggiungo al cristallo un elemento pentavalente è come se aggiungessi un elettrone ; in tal caso il drogaggio e di tipo n e l'atomo aggiunto si chiama donatore.
Col drogaggio la conduzione del semiconduttore aumenta notevolmente pur restando su valori ancora ben lontani da quelli dei conduttori propriamente detti.
La percentuale di impurità da introdurre col drogaggio non deve superare certi limiti e deve mantenersi intorno ad un atomo di impurità ogni cento milioni di atomi di germanio o di Silicio.
E' bene porre in evidenza che il drogaggio mantiene il cristallo elettricamente neutro.
DROGAGGIO DI TIPO N

Solitamente per il drogaggio di tipo N si aggiungono impurità pentavalenti come il Antimonio (Sb) , l' Arsenico (As) ed il Fosforo (P) che introducono elettroni liberi che non partecipano ai legami di valenza ed aumentano la conducibilità del semiconduttore; non vengono create lacune.
Questi atomi pentavalenti vengono chiamati "DONATORI" (vedi fig.3).
I semiconduttori drogati di tipo N hanno una conduzione maggiore di quella dei semiconduttori drogati di tipo P.
In un semiconduttore di tipo N alla conduzione dei portatori N e P del cristallo puro si sommano i portatori N degli atomi dell'impurità pentavalente, infatti le lacune costituite dallo ione positivo dell'impurità rimangono immobili in quanto i quattro elettroni ad esse rimasti rendono difficile lo spostamento degli atomi confinanti.
nel complesso quindi non si ha più un ugual numero di portatori P ed N ma i portatori N saranno molto più numerosi e saranno i portatori maggioritari rispetto ai P che saranno quindi minoritari.
Dopo il drogaggio avrò dunque:
- per ogni atomo pentavalente un elettrone disponibile per la conduzione;
- uno ione positivo fisso,, cioè non disponibile per la conduzione;
- non si creerà alcuna lacuna..
Relativamente al numero dei portatori n si avrà:
N= ND + Ni
Quanto vale questo numero?
Per determinarlo si utilizza " la legge di azione di massa "
Applicandola al nostro caso posso affermare che, in condizioni di equilibrio :
Il tasso di generazione delle cariche negative è uguale al tasso di ricombinazione.
(si ha ricombinazione quando un elettrone ed una lacuna si incontrano annullandosi a vicenda).
Ora il tasso (n° di eventi al secondo) di generazione dipende solo dalla temperatura è cioè una f(T) ; il tasso di ricombinazione è invece proporzionale a N e a P.
Possiamo allora scrivere:
f(T) = k NP
da questa espressione deriva:
f(T)/K = fi(T) = NP
ora poiché il tasso di generazione dipende solo dalla temperatura e non dal numero di cariche già presenti né dal drogaggio posso dire che ci troviamo nella medesima condizione di un semiconduttore intrinseco e cioè
N=P=Ni
Allora la nostra espressione diventa :
NP = fi(T) = Ni2
Ora, poiché nella grande maggioranza dei casi ND ≈ 1018 /cm3 ed Ni ≈ 1010/cm3 posso dire che ND>>Ni e quindi scrivere:
N ≈ ND
ed allora sarà ND P = Ni2 e quindi :
P ≈ Ni2 /ND
da queste due ultime espressioni si nota che se ND = 1018 /cm3 e Ni = 1010/cm3
sarà P= 102 /cm3 .
cioè il numero delle lacune disponibili per la conduzione sarà trascurabile rispetto a quello degli elettroni , inoltre una piccola parte di elettroni si ricombinerà con le poche lacune ed entrambi spariranno ; in questa situazione non avrò più lacune e nel contempo non mi accorgerò della diminuzione degli elettroni.
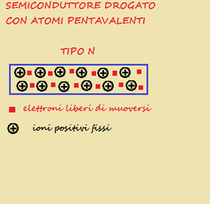
Il semiconduttore drogato di tipo N si presenterà come in fig.3a .
gli ioni positivi fissi derivano dagli atomi donatori pentavalenti che perdono un elettrone che, essendo libero di muoversi, sarà disponibile per la conduzione .
Nel processo di drogaggio non si formerà alcuna lacuna.
DROGAGGIO DI TIPO P

Solitamente per il drogaggio di tipo P si aggiungono impurità trivalenti come il Boro (B) , l' Alluminio (Al) ed il Gallio (Ga) che creano delle assenze di elettroni (lacune) che aumentano la conducibilità del semiconduttore; .
Questi atomi trivalenti vengono chiamati "ACCETTORI" (vedi fig.4)
I semiconduttori drogati di tipo P hanno una conduzione minore di quella dei semiconduttori drogati di tipo N.
In un semiconduttore di tipo P alla conduzione dei portatori N e P del cristallo puro si sommano i portatori P degli atomi dell'impurità trivalente, . nel complesso quindi non si ha più un ugual numero di portatori P ed N ma i portatori P saranno molto più numerosi e saranno i portatori maggioritari rispetto ai N che saranno quindi minoritari.
Dopo il drogaggio di tipo P avrò dunque:
- per ogni atomo trivalente una lacuna disponibile per la conduzione;
- uno ione negativo fisso, cioè non disponibile per la conduzione;
- non si creerà alcun elettrone libero.
Relativamente al numero dei portatori P si avrà:
P= NA + Ni
Quanto vale questo numero?
Per determinarlo si utilizza " la legge di azione di massa "
Applicandola al nostro caso posso affermare che, in condizioni di equilibrio :
Il tasso di generazione delle cariche negative è uguale al tasso di ricombinazione.
(si ha ricombinazione quando un elettrone ed una lacuna si incontrano annullandosi a vicenda).
Ora il tasso (n° di eventi al secondo) di generazione dipende solo dalla temperatura è cioè una f(T) ; il tasso di ricombinazione è invece proporzionale a N e a P.
Possiamo allora scrivere:
f(T) = k NP
da questa espressione deriva:
f(T)/K = fi(T) = NP
ora poiché il tasso di generazione dipende solo dalla temperatura e non dal numero di cariche già presenti né dal drogaggio posso dire che ci troviamo nella medesima condizione di un semiconduttore intrinseco e cioè
N=P=Ni
Allora la nostra espressione diventa :
NP = fi(T) = Ni2
Ora, poiché nella grande maggioranza dei casi NA ≈ 1018 /cm3 ed Ni ≈ 1010/cm3 posso dire che NA>>Ni e quindi scrivere:
P ≈ NA
ed allora sarà ND P = Ni2 e quindi :
N ≈ Ni2 /NA
da queste due ultime espressioni si nota che se NA= 1018 /cm3 e Ni = 1010/cm3
sarà N= 102 /cm3 .
cioè il numero degli elettroni disponibili per la conduzione sarà trascurabile rispetto a quello delle lacune , inoltre una piccola parte delle lacune si ricombinerà con i pochi elettroni disponibili per la conduzione, ed entrambi spariranno ; in questa situazione non avrò più elettroni disponibili per la conduzione e nel contempo non mi accorgerò della diminuzione delle lacune.

Il semiconduttore drogato di tipo P si presenterà come in fig.4a . gli ioni negativi fissi derivano dagli atomi accettori trivalenti che acquisiscono un elettrone accettando un elettrone di valenza di un atomo attiguo formando pertanto una lacuna libera di muoversi, che sarà disponibile per la conduzione . Nel processo di drogaggio non si formerà alcun elettrone libero
GIUNZIONE NP
Prendiamo due semiconduttori estrinseci, uno drogato P ed uno drogato N come mostrato in fig.5.
In quello drogato N ci saranno nella banda di conduzione degli elettroni derivanti dagli atomi donatori (portatori N maggioritari azzurri di fig.5) e gli elettroni del semiconduttore intrinseco (portatori N maggioritari rossi di fig.5).
Saranno poi disponibili per la conduzione anche le lacune derivanti dal semiconduttore intrinseco (portatori P minoritari rossi di fig.5); invece, come già detto, le lacune derivanti dall'intoduzione delle impurità pentavalenti non saranno disponibili (ioni positivi fissi, (vedi fig.3a)) per la conduzione.
In quello drogato P ci saranno disponibili per la conduzione le lacune derivanti dagli atomi accettori (portatori P maggioritari verdi di fig.5) e le lacune del semiconduttore intrinseco (portatori P maggioritari arancioni di fig.5).
Saranno poi disponibili per la conduzione anche gli elettroni derivanti dal semiconduttore intrinseco (portatori N minoritari arancioni di fig.5).

Se ora formiamo, come in fig.5, una giunzione NP i portatori N (elettroni) si diffonderanno verso il semiconduttore P e le lacune P si diffonderanno verso il semiconduttore N.
i primi si lasceranno indietro degli ioni positivi ed i secondi degli ioni negativi che si posizioneranno come indicato in fig.5 formando una zona priva di cariche chiamata zona di svuotamento.
questa zona di svuotamento impedirà ad altri elettroni di passare nel semiconduttore P e ad altre lacune di passare nel semiconduttore N.
Per permettere un ulteriore passaggio di cariche bisogna superare una certa differenza di potenziale che è propria della zona di svuotamento e dipende dal semiconduttore .
Nel Silicio questa differenza di potenziale è pari a circa 0,7V, nel Germanio a 0,2 V.
Quanto detto in merito alla barriera di potenziale che si forma in corrispondenza della giunzione lo si può comprendere meglio osservando la fig.5a
Per comodità pensiamo alle due zone P ed N separate (in realtà la giunzione non si ottiene unendo le due sezioni) come in fig.5a a), in esse si notano gli ioni fissi e le cariche mobili.
Finché le due sezioni P ed N sono separate non esistono zone dove prevalga un segno o l'altro (non esistono zone di svuotamento, tutti gli ioni cioè sono compensati) ma quando unisco le due sezioni la parte P del giunto diventa negativa in quanto i suoi ioni negativi fissi non hanno nelle vicinanze lacune che si stanno diffondendo verso la parte N del giunto (questa parte del giunto si sta svuotando di cariche positive); cosa succede nella parte N del giunto? succede la stessa cosa a segno invertito e cioè la parte N del giunto diventa positiva in quanto i suoi ioni positivi fissi non hanno nelle vicinanze elettroni( non sono compensati) che si stanno diffondendo verso la parte P del giunto (questa parte del giunto si sta svuotando di cariche negative.)
in prossimità del giunto insomma a causa della diffusione delle lacune nella zona N e degli elettroni nella zona P si forma una zona priva di cariche mobili e rimangono solo ioni positivi nella parte N e ioni negativi nella parte P.
Si crea dunque una zona con carica negativa nella parte P ed una zona con carica positiva nella zona N (vedi fig.5a c)
Si crea un campo elettrico che è legato a ρ, εo, εr ( nell' ordine: densità di carica , costante dielettrica nel vuoto, costante dielettrica relativa) nella seguente espressione:
dE/dx = ρ/εoεr
integrando si ottiene il campo il cui grafico è riportato
in fig.5a d).
si crea inoltre una barriera di potenziale che è legato al campo elettrico secondo la formula:
dΦ/dx=-E
integrando si ottiene il potenziale il cui grafico è riportato in fig.5a e).
La larghezza della zona di svuotamento aumenta con la diffusione la quale però fa aumentare la carica il campo e la barriera di potenziale (in breve la larghezza della zona) ; ciò frena la diffusione finché si arriva ad un punto in cui la diffusione si ferma.
Ciò accade quando l'energia potenziale dei portatori di carica è inferiore a quella della barriera formatasi.
DIODO
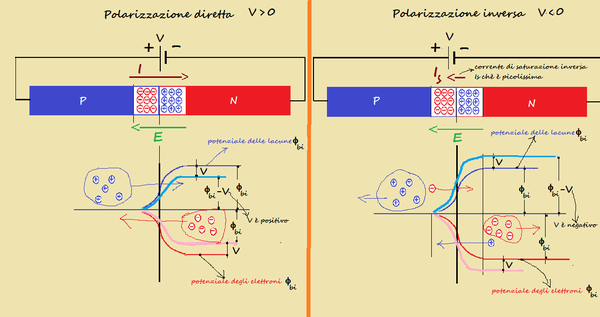
La giunzione NP è un diodo che costituisce una continuità (permette la circolazione della corrente) o una interruzione (impedisce la circolazione della corrente) a seconda di come è polarizzato. in fig.6 a) è illustrata la polarizzazione inversa in fig.6 b) quella diretta di un diodo.
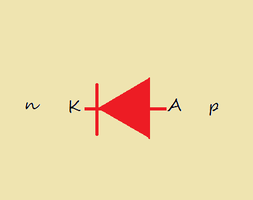
Nella fig 6 è indicato il simbolo del diodo; la corrente scorre dall'anodo A al catodo K.
Se osserviamo la fig.6a-a) (POLARIZZAZIONE INVERSA) ci rendiamo conto che il tipo di polarizzazione inversa allontana i portatori N maggioritari (vedi freccia azzurra di fig.6a-a) e i portatori P maggioritari (vedi freccia verde di fig.6a- a) dalla giunzione che non viene dunque attraversata dalla corrente.
In realtà una piccola corrente attraversa la giunzione, questa è dovuta ai portatori P (vedi freccia rossa di fig.6a-a) ed N (vedi freccia arancione di fig.6a-a) minoritari; questa piccola corrente viene chiamata corrente di saturazione inversa Is.
Se osserviamo invece la fig.6a-b) (POLARIZZAZIONE DIRETTA) ci rendiamo conto che il tipo di polarizzazione diretta avvicina i portatori N maggioritari (vedi freccia azzurra di fig.6a- b) e i portatori P maggioritari (vedi freccia verde di fig.6a- b) alla giunzione che viene dunque attraversata dalla corrente. a questa va sottratta la trascurabile corrente dovuta ai portatori P (vedi freccia rossa di fig.6a-b) ed N (vedi freccia arancione di fig.6a-b) minoritari.
Ricapitolando:
Un semiconduttore P è costituito da ioni negativi fissi derivanti dagli atomi accettori trivalenti che inglobano un elettrone, da lacune maggioritarie e da elettroni minoritari; il semiconduttore così drogato è neutro in quanto tutti gli ioni fissi sono compensati dalle lacune.
Un semiconduttore N è costituito da ioni positivi fissi derivanti dagli atomi donatori pentavalenti che cedono un elettrone , da elettroni maggioritari e da lacune minoritarie; il semiconduttore così drogato è neutro in quanto tutti gli ioni fissi sono compensati da elettroni.
Quando viene creata una giunzione PN succede che lacune della zona N diffondono nella zona P e poi ricombinano ed elettroni della zona N diffondono nella zona P e poi ricombinano..
in questo passaggio di lacune ed elettroni in prossimità della giunzione si crea una zona di carica spaziale costituita da ioni fissi negativi nella parte P e da ioni fissi positivi nella parte N, si crea questa zona di carica perché gli ioni in quella ristretta zona non risultano più compensati da lacune /elettroni che si stanno diffondendo le prime verso la zona N e i secondi verso la zona P.
Le dimensioni di questa zona, chiamata anche zona di svuotamento, variano .
crescono sempre più lentamente finché cessano di crescere e la diffusione si arresta.
Le altre due zone a sinistra (azzurra) e a destra (rossa) sono due zone neutre dove gli ioni fissi sono tutti compensati.
Nella fig.6a1 è indicato cosa succede nella giunzione NP quando non è polarizzata.
Nella fig.6b è rappresentato ciò che succede invece nel caso della polarizzazione diretta ed inversa .
POLARIZZAZIONE DIRETTA
La parte sinistra della fig.6b rappresenta la polarizzazione diretta del diodo, infatti risulta V > 0.
Nella zona di svuotamento nasce un campo elettrico E che ha il verso della freccia verde che si oppone alla diffusione delle lacune nella zona N ed alla diffusione degli elettroni nella zona P.(le lacune si muovono nella direzione del campo e gli elettroni in senso opposto al campo). le curve azzurra e rossa rappresentano la barriera di potenziale delle lacune e degli elettroni che impedisce alle lacune ed agli elettroni di attraversare la giunzione.
Quando polarizzo direttamente la giunzione PN (V > 0) succede che la barriera si abbassa permettendo così alle lacune ed agli elettroni di attraversare la giunzione.
le due barriere di potenziale abbassate sono indicate dalle curve celeste e rosa.
Ora si può pensare che riprendendo la diffusione il campo aumenti e che di conseguenza la diffusione e quindi la corrente tenda a cessare.
Così non è infatti la polarizzazione mantiene il potenziale al valore (Φ ib - V).
POLARIZZAZIONE INVERSA
La parte destra della fig.6b rappresenta la polarizzazione inversa del diodo, infatti risulta V > 0.
Nella zona di svuotamento nasce un campo elettrico E che ha il verso della freccia verde che si oppone alla diffusione delle lacune nella zona N ed alla diffusione degli elettroni nella zona P.(le lacune si muovono nella direzione del campo e gli elettroni in senso opposto al campo). le curve azzurra e rossa rappresentano la barriera di potenziale delle lacune e degli elettroni che impedisce alle lacune ed agli elettroni di attraversare la giunzione.
Quando polarizzo inversamente la giunzione PN (V< 0) succede che la barriera si solleva impedendo ancora di più alle lacune ed agli elettroni di attraversare la giunzione.
le due barriere di potenziale incrementate sono indicate dalle curve celeste e rosa.
Non dovrebbe in tal modo scorrere alcuna corrente attraverso la giunzione in realtà c'è una piccolissima corrente Is dovuta alle lacune minoritarie della zona N ed agli elettroni minoritari della zona P.
Nella parte destra della fig.6b si nota chiaramente come queste lacune ed elettroni minoritari sono spinti dal campo E ad attraversare la giunzione.
DIODO IDEALE

Abbiamo detto che il diodo costituisce una continuità (permette la circolazione della corrente) o una interruzione (impedisce la circolazione della corrente) a seconda di come è polarizzato.
Un diodo ideale pertanto ha una caratteristica come la spezzata marrone di fig 6c .
Consideriamo il circuito di fig.6c con un generatore Vs sinusoidale , un diodo la cui tensione chiamiamo Vd ed una resistenza R percorsa dalla corrente I.
La relazione esterna del circuito è: Vs = Vd + RI la relazione interna I(Vd ) è quella che lega la corrente I alla tensione Vd ; le due incognite sono I e Vd ; il sistema non è lineare,. ( I(Vd ) infatti è una curva esponenziale come vedremo inseguito.
Nel diodo ideale però la caratteristica è quella a tratti marrone di fig.6c , non è esponenziale..
su questa caratteristica a tratti disegno la retta di carico rappresentata dalla relazione esterna e disegno la famiglia di rette blu; che trattasi di una famiglia di rette è evidente infatti le rette di carico sono tante rette quanti sono i valori di Vs . che varia fra -Vsmax e + Vs max.
La prima retta a destra ha espressione :
Vsmax = Vd + RI e quindi per I = 0 → Vsmax = Vd
per Vd = 0 → I = Vsmax / R
l'ultima retta a sinistra ha espressione :
-Vsmax = Vd + Ri e quindi per I = 0 → -Vsmax = Vd
per Vd = 0 → I = -Vsmax /R
Osservando la famiglia di rette e la caratteristica a tratti marrone posso scrivere:
se Vs > 0 → Vd = 0 → Vd = RI = Vu
se Vs < 0 → I = 0 → Vd = 0 =Vu
Ottengo allora il grafico ultimo a destra dove le alternanze negative di Vs sono scomparse.
si è ottenuto cioè il raddrizzamento della tensione sinusoidale Vs.
CURVA CARATTERISTICA DEL DIODO REALE

Nella realtà la curva caratteristica del diodo è quella rappresentata in fig.7.
La corrente circolante in un diodo reale è :
I= Is (e V/ηVT - 1) dove
Is è il valore della corrente inversa di saturazione ;
q è la carica dell'elettrone uguale a
1,6 x 10-19 coulomb;
V è il potenziale applicato;
η è il fattore di idealità il cui valore è compreso fra 1 e 2 ;
VT = K.T /q è la tensione di temperatura dove
T è la temperatura assoluta del diodo,
K la costante di Boltzman pari a 1,38 x 10-23 Joule/°K
ed e è il numero di Eulero pari a 2,7183...
A temperatura ambiente, 300 K circa la tensione di temperatura è pari a 26 mV ; cioè
VT = 26 mV
il diagramma della corrente I e mostrato in fig.7
Il diodo è polarizzato direttamente quando V è positivo; quando V è negativo il diodo è polarizzato inversamente.
Riguardo alla temperatura possiamo dire che, a tensione esterna costante, quando si ha polarizzazione diretta, un suo aumento determina una riduzione della corrente; inversamente avviene quando la polarizzazione è inversa; in questo caso il valore di Is raddoppia ad ogni aumento di 10 °C.
- Se V = 0 I = 0 e non si ha passaggio di corrente:
- Se la tensione è minore di un certo valore di soglia Vs (0,2 V per il Germanio, 0,7V per il silicio) non si ha passaggio di corrente ;
- Per valori di V maggiori di Vs si ha un aumento esponenziale della corrente;
- La tensione esterna deve mantenersi inferiore ad un valore massimo Vmax. pena danneggiamento del diodo.
- Anche per tensioni negative il diodo non conduce se non si supera un valore di soglia negativo circa uguale, in valore assoluto, a Vs;
- Per tensioni esterne più negative la corrente diventa quasi uguale a -I0 che ha un valore molto basso; questo valore rimane costante al diminuire della tensione inversa applicata;
- Raggiunto un determinato valore di tensione inversa Vz (tensione di Zener) la corrente inversa raggiunge valori molto elevati. Questo effetto Zener viene sfruttato in particolari tipi di diodi (Diodi Zener).
CAPACITA IN UN DIODO

Abbiamo visto che la zona di svuotam,ento che assume l'aspetto di fig.8 è ampia nella polarizzazione inversa e ristretta nella polarizzazione diretta.
Il diodo come si nota in fig.8 si comporta come un condensatore .
Ha una capacità di qualche micro Farad nella polarizzazione diretta e di pochi pico Farad nella polarizzazione inversa.
RESISTENZA DI UN DIODO
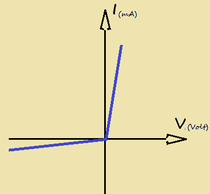
Con un tester posso misurare la resistenza statica di un diodo che è bassa nella polarizzazione diretta (qualche decina di Ohm) ed alta nella polarizzazione inversa (qualche centinaio di K Ohm).
Queste misure non hanno alcuna importanza nella progettazione di un diodo , servono unicamente per verificare che il diodo funzioni correttamente.
Dalla fig.9 posso calcolare il valore della resistenza statica in polarizzazione diretta ed inversa.
.

il diagramma di fig.7 in pratica viene rappresentato come in fig.10, infatti la corrente I0 è molto bassa.
Dal diagramma di fig. 10 posso ricavare il valore della resistenza dinamica del diodo che nella realtà non segue la legge di Ohm.
la resistenza pari a (V2-V1)/ (I2-I1) varia al variare di V1, V2, I2, I1 .
DIODO LED
Nella fig.11 è rappresentato un circuito con un diodo LED.
nel circuito è bene porre sempre una resistenza per evitare che il diodo si distrugga.
Il calcolo della resistenza è riportato in fig. 11 dove sono indicati anche i valori delle tensioni nominali, a seconda del colore, e quello della corrente nominale.
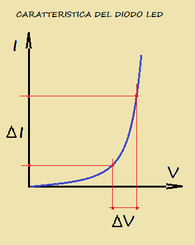
La necessità della resistenza si capisce guardando la caratteristica del diodo LED riportata in fig.12
infatti ad un piccolo incremento della tensione corrisponde un incremento notevole della corrente.
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta