ANTENNA WINDOM
Ho realizzato, nel giardino di casa un' antenna WINDOM
come indicato in fig.1
Le sue dimensioni sono riportate in fig.2
Ho realizzato Il necessario Balun 6:1 come mostrato in fig. 3
calcolo balun 6;1
L'antenna può sintonizzare le seguenti frequenze : 3,6 - 7,2 - 14,4 - 21,4 -28,8 Mhz.
L'impedenza nel punto d'incontro dei due rami dell'antenna è pari a 300 Ω ; l'impedenza del coassiale di collegamento con la radio è pari a 50 Ω.
L'induttanza lato antenna è : La = 300 x 5/(2π 3.600.000) = 66 μH
L'induttanza lato coassiale è : Lc = 50 x 5/(2π 3.600.000) = 11 μH
Con una bacchetta di ferrite e 10 spire di trifilare posizionati come in fig.3 ho ottenuto proprio le induttanze calcolate.
Il balun costruito è un 6:1 infatti , 66/11 =6 ; lo stesso risultato si ottiene dividendo il numero delle spire fra il punto A ed il punto D (24,5) per il numero delle spire fra il punto B ed il punto C (10) ed elevando il risultato al quadrato (24,5/10)2= 6
calcolo della potenza
Come già detto in precedenza nel capitolo "balun"( calcolo della potenza con balun in ferrite") parte dell'energia in transito si trasforma in calore e questo se è eccessivo può procurare la rottura del nucleo del balun.
vediamo di verificare la potenza applicabile alla mia antenna Windom.
La bacchetta in ferrite da me utilizzata ha una sezione di 0,78 cm2; supponiamo di voler trasmettere una potenza di 100W e che l'antenna butti fuori tutti i 100 W; in queste condizioni la tensione nel trasmettitore vale Et : √(100x50)= 70V mentre quella nell'antenna vale Ea : √(100x300) = 173V.
Poiché conosco le tensioni , il numero delle spire (24,5:10) e la sezione della ferrite posso calcolare la densità di flusso (induzione magnetica) utilizzando la formula:
B max = (E x 102)/(4,44 x An x N x f)
B max = (70 x 102)/(4,44x0,78x10xf)=(173x102)/(4,44x0,78x24,5xf)
per f= 0,1 MHz B max = 2021 gauss
per f= 1 MHz B max = 202 gauss
per f=7 MHz B max = 28,87 gauss
per f=14 MHz B max = 14,43 gauss
per f= 21 MHz B max = 9,62 gauss
per f= 28 MHz B max = 7,22 gauss
Si possono fare le dovute considerazioni osservando la tabella sottostante che contiene i valori ammissibili di densità di flusso in funzione della frequenza

ANTENNA FILARE
Ho realizzato anche un'antenna filare come indicato in fig.4
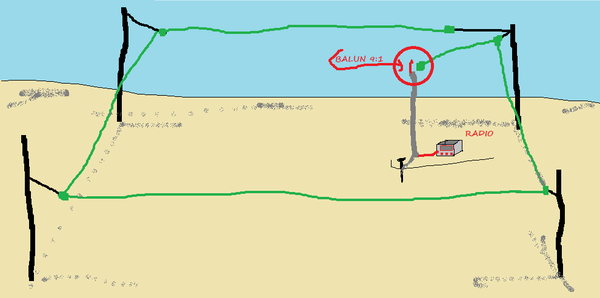
Le sue dimensioni sono riportate in fig.5

Poiché l'impedenza dell'antenna è pari a 450 Ω e quella del coassiale è pari a 50 Ω ho inserito un balun 9:1 (450/50) disegnato in fig. 6

calcolo balun 9:1
Trattasi di un'antenna multibanda.
L'impedenza dell'antenna è pari a 450 Ω ; l'impedenza del coassiale di collegamento con la radio è pari a 50 Ω.
L'induttanza lato antenna è :
La = 450 x 5/(2π 1.000.000) = 358 μH
L'induttanza lato coassiale è :
Lc = 50 x 5/(2π 1.000.000) = 40 μH
Con un toroide amidon FT240-43, per ottenere quelle induttanze sono necessarie 18 spire per il primario e 6 spire per il secondario come mostrato in fig. 6.
Per il calcolo si è utilizzata la tabelle che trovasi nel sito internet "toroids.info". In corrispondenza del toroide FT240-43 si trova il valore di Al pari a 1075; ricordando la formula riportata nel capitolo "balun" si ricava il numero delle spire del primario e del secondario.
Np= √(La x 1000/Al)
Ns = √(La x 1000/Al)
calcolo della potenza
Come già detto in precedenza nel capitolo "balun"( calcolo della potenza con balun in ferrite") parte dell'energia in transito si trasforma in calore e questo se è eccessivo può procurare la rottura del nucleo del balun.
vediamo di verificare la potenza applicabile alla mia antenna filare.
Il toroide utilizzato FT-240-43 ha una sezione A di 1,57 cm2;
supponiamo di voler trasmettere una potenza di 100W e che l'antenna butti fuori tutti i 100 W; in queste condizioni la tensione nel trasmettitore vale Et : √(Wx50)= 70V mentre quella nell'antenna vale Ea : √(Wx450) = 212V.
Poiché conosco le tensioni , il numero delle spire (18:6) e la sezione del toroide posso calcolare la densità di flusso utilizzando la formula:
B max = (E x 102)/(4,44 x An x N x f)
B max = (70 x 102)/(4,44x1,57x6 x f)=(212x102)/(4,44x1,57x18xf)
per f= 0,1 MHz B max = 1674 gauss
per f= 1 MHz B max = 167 gauss
per f=7 MHz B max = 23,9 gauss
per f=14 MHz B max = 11,95 gauss
per f= 21 MHz B max = 7,96 gauss
per f= 28 MHz B max = 5,97 gauss
Si possono fare le dovute considerazioni osservando la tabella sottostante che contiene i valori ammissibili di densità di flusso in funzione della frequenza.

Antenna magnetica amplificata
Avete problemi d'antenna con le vostre vecchiette a modulazione d'ampiezza onde lunghe e medie? provate questo progetto preso da "le Radio di Sophie" realizzato da Stefano Canavesi.
Io l'ho fatto ed ho ottenuto ottimi risultati.

prove d'ascolto

La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta





