retta di carico
In generale la retta di carico ( in verde nella fig.2) è definita come la rappresentazione grafica del secondo principio di Kirchhoff applicato alla rete di uscita del dispositivo.

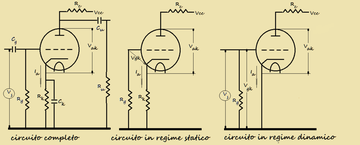
Facendo riferimento alla fig.1, dove è rappresentato il circuito completo di un triodo e la schematizzazione dello stesso in regime statico e dinamico, posso definire, la retta di carico nei due regimi nel modo seguente:
regime statico
Applicando Kirchhoff alla rete d' uscita del triodo ( vedi parte centrale della fig.1) otteniamo:
Vcc= Ia ( Rc + Rk ) + Vak da cui :
Ia = -Vak / ( Rc + Rk ) + Vcc / ( Rc + Rk ) .
Quest'ultima equazione rapprenta una retta nella forma:
y = mx + q ;
in essa m = - 1/ ( Rc + Rk ).
La retta è disegnata in verde (retta (a)) nella fig.2.
m rappresenta il coefficiente angolare della retta cioè la tangente dell'angolo formato dalla retta col verso positivo dell'asse delle ascisse) .
regime dinamico
Applicando Kirchhoff alla rete d' uscita del triodo ( vedi parte destra della fig.1) otteniamo:
Vcc =Ia Rc+ Vak; da cui :
Ia = -Vak / Rc + Vcc / Rc .
Anche questa equazione rapprenta una retta nella forma:
y = mx + q ;
in essa m = - 1/ Rc
ed è disegnata in rosso nella fig.2.
Nel caso dinamico il denominatore del coefficiente m è diminuito rispetto a quello statico e la retta (b) rossa di fig.2
risulta ruotata rispetto alla verde (a) in senso orario; ruota ancora in senso orario se i morsetti
d'uscita vengono chiusi su di un carico resistivo Ru.
Infatti, in quest'ultimo caso, risulta: m=-1/ (Rc//Ru), quindi il denominatore di m è ancora minore dei casi precedenti (vedi retta rossa (c) di fig.2.).
La retta di carico dinamica ha un'importanza notevole infatti in corrispondenza delle variazioni imposte dal segnale in arrivo, il punto di lavoro non si sposta lungo la retta statica, ma su quella dinamica.
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta


