Reazione

In fig.1 è rappresentato un segnale in ingresso V_i, un nodo di comparazione NC, un amplificatore ed un blocco di reazione.

Quota parte di V_u, dopo aver attraversato il blocco di reazione, si ripresenta all'ingresso dell'amplificatore dove viene sommato algebricamente, nel nodo NC, col segnale in ingresso V_i.

Siamo in presenza di una retroazione di tensione.

La tensione V_r è pari a V_u x β dove β rappresenta il fattore di reazione.

Il nodo NC provvede a sommare algebricamente V_r e V_i ottenendo V_e.

Se V_r è in fase con V_i (ha lo stesso segno di V_i) sono in presenza di una reazione positiva, in caso contrario, negativa.

amplificazione senza reazione

In caso di amplificazione senza reazione il guadagno è pari a :

A= V_u/V_e.

amplificazione con reazione

Nel caso di amplificazione con reazione il guadagno è pari a :

A_r=V_u/V_i = V_u/ V_e-V_r = V_u/ V_e - βV_u ;

dividendo il numeratore ed il denominatore per V_e ottengo:

A_r= A/1-βA.

reazione negativa

Nel caso in cui 1-βA > 1 , che corrisponde a βA < 0, sono in presenza di reazione negativa infatti in tal caso Ar è inferiore ad A (Vr non è in fase con Vi);

La reazione negativa è frequentemente utilizzata nella progettazione degli amplificatori infatti la perdita di guadagno è compensata da molti vantaggi che si possono ottenere e che sono:

stabilità dell'amplificazione

La stabilità dell'amplificazione può essere misurata dal rapporto:

ΔAmplificazione /Amplificazione cioè dalla variazione relativa dell'amplificazione ; minore è il Δ maggiore è la stabilità dell'amplificazione. Vediamo allora di confrontare la variazione relativa dell'amplificazione nel caso di amplificazione senza reazione negativa (dA/A) con quella che si riferisce all'amplificazione con reazione negativa ( dA_r/A_r).

Sappiamo che :

A_r= A/1-βA , derivando otteniamo:

dA_r= dA/(1-βA)²(ricordiamo che df(x)/dg(x) = (f '(x)g(x) -g'(x)f(x))/g(x)²)

si ottiene dA_r/A_{r =}dA/ (A (1-βA))

Ora, poichè siamo in reazione negativa e quindi (1-βA) > 0

si ottiene : dA_r/A_{r
<}dA/A cioè in presenza di retroazione negativa la stabilità dell'amplificazione migliora.

aumento del rapporto segnale rumore

Al segnale utile in uscita si possono sovrapporre dei rumori (noise) (ripple dell'alimentazione, campi elettromagnetici, derive termiche, rumore dei componenti ecc..).

se faccio il rapporto fra il segnale ed il rumore , S/N ottengo un numero espresso in decibel che mi da una misura del corretto funzionamento dell'amplificatore; più alto è questo numero migliore è il funzionamento

Con un rumore V_n come in fig.2 , a parità di segnale di ingresso ed in assenza di retroazione ho:

V_r= 0 , V_e= V_i , V_u= AV_e + V_n = AV₁ + V_n ; S/N = AV_i/V_n.

a parità di segnale di ingresso ed in presenza di retroazione ho::

V_u= AV_e + V_n= A(V_i +V_r ) + V_n= A(V_i +βV_u ) + V_nda cui :

V_u= AV_i/(1-Aβ) +V_n/(1-Aβ)

poiché il primo termine di quest'ultima espressione rappresenta il segnale utile ed il secondo il rumore possiamo scrivere AV_i/(1-Aβ) /V_n/(1-Aβ) = S/N = AV_i/V_n

l'espressione trovata è uguale a quella relativa al caso di assenza di retroazione ; possiamo pertanto dire che:

a parità di segnale di ingresso il rapporto S/N con o senza reazione rimane invariato.

Il segnale d'uscita rispetto al caso senza reazione è ridotto di un fattore 1-Aβ.

a parità di segnale di uscita ed in presenza di retroazione ho:

V_u= AV_e + V_n= A(V_i (1-Aβ) +V_r ) + V_n= A(V_i(1-Aβ) +βV_u ) + V_nda cui :

V_u= AV_i +V_n/(1-Aβ);

poiché il primo termine di quest'ultima espressione rappresenta il segnale utile ed il secondo il rumore possiamo scrivere relativamente a S/N:

S/N= (AV_i /V_n)x(1-Aβ)

_{Quindi a parità di segnale di uscita il rapporto S/N con reazione negativa aumenta di
un fattore 1-Aβ}

riduzione della distorsione armonica

Quando vengono interessate zone a funzionamento non lineare degli amplificatori si producono delle distorsioni .

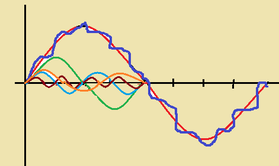
il segnale distorto (linea azzurra di fig.3 ) è dato dalla somma di sinusoidi (armoniche) aventi frequenza doppia tripla quadrupla.......... della fondamentale .

Se elimino tutte le armoniche ottengo una sinusoide (linea rossa) che rappresenta il segnale non distorto.

Tutte queste armoniche possono essere viste come dei segnali di rumore.

Ricadiamo allora nel caso precedente .

Cioè , anche in questo caso, la retroazione negativa riduce, a parità del segnale di uscita, il rumore (le armoniche ) di un fattore _{1-Aβ , o , che è lo stesso, aumenta, dello stesso fattore, il rapporto
S/N.}

reazione positiva

Nel caso invece in cui 1-βA < 1 ,che corrisponde a βA > 0, sono in presenza di reazione positiva, in tal caso infatti Ar è maggiore di A (Vr è in fase con Vi).

la reazione in un circuito oscillatorio LC Triodo

Prendiamo in considerazione il circuito di fig.2 costituito da un triodo e da un circuito oscillante L₁ C₁. analizziamo i casi a, b, c, d.

caso a)

Se il circuito L₁ C₁ è isolato (non c'è il triodo) l'oscillazione ha una smorzamento naturale ( vedi "circuito oscillatorio") causato dalla presenza della resistenza positiva R_p indicata nel circuito equivalente ; in questo caso la resistenza negativa R_n non esiste..

caso b)

Se il circuito L₁ C₁è collegato al triodo come mostrato in fig.2 succede che l'oscillazione prodotta iniettata in griglia subisce una amplificazione e dalla placca passa all'induttanza L₂ che è accoppiata in modo variabile all'induttanza L1 nella quale induce una corrente che, se ha la stessa frequenza ed è in fase con quella oscillante presente nel circuito L₁ C₁(reazione positiva) restituice al circuito oscillante parte della energia persa; è come se comparisse una resistenza negativa R_n che si somma algebricamente a quella positiva R_p .

In questo caso la comparsa di R_nfa in modo che lo smorzamento indicato in fig.2b sia minore di quello naturale

caso c)

Incrementando l'accoppiamento fra L2 ed L3 la resistenza negativa arriva ad eguagliare quella positiva ed il circuito privo di resistenza diviene molto sensibile.

caso d)

Un ulteriore incremento dell'accoppiamento porta ad una resistenza complessiva negativa; l'ampiezza delle oscillazioni aumenta finché non rimangono costanti in quanto la valvola entra in saturazione .

oscillatori

riprendiamo l'espressione dell'amplificazione con reazione:

Ar= Vu/Vi = A / 1-βA.

Se si verifica che 1-βA. = 0 sarà Ar = ∞

ma Ar = ∞ può significare due cose :

Vu = ∞ il che è fisicamente impossibile;
Vi = 0

Nel secondo caso senza alcun segnale in ingresso (Vi = 0) ho un segnale in uscita.

Ci troviamo cioè difronte ad un generatore.

La condizione βA = 1 chiamata "Condizioine di Barkhausen" è necessaria per ottenere un generatore di segnali che possono essere :

Oscillatori , se generano segnali sinusoidali;
generatori di forme d'onda se generano tutti gli altri tipi di forme d'onda.