Il magnetismo è un particolare stato fisico dei materiali ferrosi i quali presentano proprietà di attrazione e repulsione reciproca; in sostanza un magnete o una sostanza magnetizzata influenza la parte di spazio circostante mediante una forza che fa sentire i propri effetti ad altre sostanze magnetiche o magnetizzabili presenti in questo spazio; questa porzione di spazio influenzato dalla sostanza magnetica si chiama campo magnetico.
Un magnete, per quanto possa dividerlo in due parte, possiede sempre due poli : Nord e sud ; il campo magnetico creato dal magnete è rappresentato da linee di forze (fig.1) che escono dal polo Nord ed entrano nel polo sud; Il campo magnetico è rappresentato dal vettore H tangente alle linee di forza.

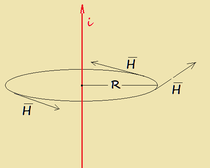
Quando un conduttore elettrico è percorso da una corrente i genera un campo magnetico H nello spazio circostante; se il conduttore è rettilineo il vettore campo magnetico è : 

H = i/2πR ;

esso è tangente alle linee di forza, giace sul piano ad esso perpendicolare ed ha il verso di una vite destrorsa che avanza nel senso di scorrimento della corrente (regola della mano destra); in tale formula R è la distanza dal conduttore del punto su cui si calcola il campo H,,  i è la corrente (fig.2).

se moltiplico per μ_o (permeabilità magnetica nel vuoto ) il primo ed il secondo temine dell'espressione su indicata ottengo:

Hμ_o  = μ_o i/2πR  = B

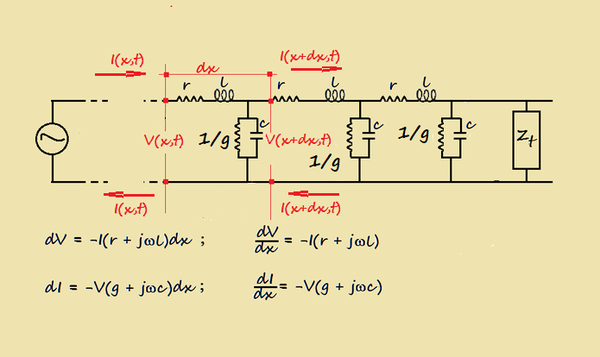
Nel caso di una spira circolare percorsa da corrente (fig.3) il campo elettromagnetico H generato, misurato al centro della spira o in un punto B posto nell'asse della spira, è pari rispettivamente a.:

 

 

• al centro della spira :  H = i/2R;
• in un punto B sull'asse della spira: H = iR²/2(z²+R²)^3/2 .

 

Nelle formule i è la corrente, R il raggio  della spira e z la distanza del punto B dal centro della spira.

Nel caso di un solenoide (più spire successive disposte in serie) (fig.4) il campo H ha verso prevalente lungo l'asse del solenoide e vale  N.i / l e viene misurato in amperspire / metro; nella formula N è il numero di spire, i è la corrente ed l la lunghezza del solenoide.

Nel caso di un solenoide toroidale (fig.5), la cui principale caratteristiche è quella di contenere tutto il campo al suo interno, se N è il numero delle spire, R la lunghezza del raggio medio ed i la corrente, sara:

H = Ni / 2πR.

Nella seconda metà dell'ottocento il grande fisico scozzese  Maxwell riusci a riassumere in sole 4 equazioni la descrizione di tutti i fenomeni elettromagnetici.

La grande novità della teoria di Maxwell consiste nell' aver definito il campo elettromagnetico come un qualcosa di fisico, di reale che si propaga , nello spazio alla velocità della luce (C= 300.000.000 m/s); questo concetto non era presente nella meccanica classica.

Grazie alle equazioni di maxwel sapiamo che  il campo elettrommagnetico è rappresentato da due vettori ; il vettore E (campo elettrico) ed il vettore H (campo magnetico). La rappresentazione grafica dell'onda elettromagnetica è rappresentata in fig.7. I vettori E ed H si dispongno tangenti alle linee di forza del campo. Nella realtà le onde elettromagnetiche sono una roba abbastanza complessa; esiste un campo vicino "near field" che si comporta in un certo modo ed un campo lontano "far field" che si comporta in un 'altro...

Per un emettitore di radiofrequenze  cioè si vengono a definire sia condizioni di near firld  (campo vicino) vedi fig.7a   che di far field (campo lontano). Se la distanza dalla sorgente radiante è inferiore alla lunghezza d’onda si è in condizioni di campo vicino. In caso contrario si è in condizioni di campo lontano. In campo vicino il campo elettrico E e il campo magnetico H sono indipendenti. In campo lontano esiste un rapporto costante fra  E  ed  H , questo rapporto è l'impedenza dello spazio e vale 377Ω.

L'esempio di un motoscafo di fig.7 ci permette di avere un'idea di come è combinato il campo elettromagnertico.

Poniamo che il motore sia l'origine della radio frequenza,  l’elica girando  causerà  delle onde che nelle vicinanze dell'elica  saranno tutte incasinate (turbolernza); ciò è quanto accade nel near field dove la relazione tra campo elettrico e campo magnetico non è costante..

Lontani  dall'elica  del motoscafo le onde saranno spaziate tra di loro e regolari, ciò invece quanto accade nel far field dove c’è una relazione costante tra campo elettrico e magnetico .

In realtà il near field è suddiviso in due zone, una più vicina alla fonte che costituisce una zona di campo vicino reattivo, ed una più lontana che costituisce la zona (FRESNEL) di campo vicino radiativo.

Oltre la zona di FRESNEL , come già detto, esiste la zona di campo lontano chiamata zona di FRAUNHOFER.

Relativamente alle 3 zone possiamo dire:

 

• Nella zona di campo vicino reattivo dominano i termini quasi statici di

campo e elettrico e di campo magnetico.

E' la zona in cui l'antenna immagazzina energia elettrica e magnetica che viene scambiata, sotto forma di potenza reattiva, col generatore che la alimenta, il campo E ed il campo H non sono fra loro correlati.

La presenza di un corpo estraneo in questa zona altera fortemente le caratteristiche dell'antenna a causa del forte accoppiamento.

•  La zona di campo vicino radiativo è una zona di transizione che, per

antenne poco estese con lunghezza minori di λ non esiste..

I contributi quasi statici dei campi reattivi sono trascurabili ed  i campi H ed E sono abbastanza correlati fra di loro a mezzo dell'impedenza caratteristica.

Il campo presenta fluttuazioni spaziali dovute alle interferenze di fase tra i contributi di campo provenienti dalle diverse zone dell'antenna.

• La zona di campo lontano radiativo o zona di  Fraunhofer si estende

all'infinito.

Il campo elettromagnetico ha la caratteristica di un'onda sferica non uniforme.

I campi E ed H sono correlati fra di loro a mezzo dell'impedenza caratteristica : E/H=377Ω.

Il campo decresce con la distanza dall'antenna proporzionalmente a 1/d (d= distanza dall'antenna).

La densità di potenza decresce con la distanza dall'antenna in modo proporzionale a 1/d².

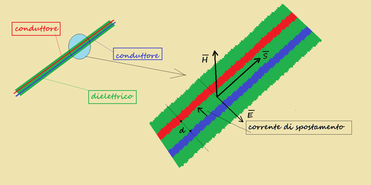
La fig. 7 mostra l'aspetto di un'onda elettromagnetica: ...ma come si forma?

Prendiamo due conduttori paralleli isolati tra loro ed applichiamo un segnale sinusoidale di una certa potenza e di frequenza f (fig.8).

Tra i due conduttori si forma un campo elettrico E sinusoidale di frequenza f che viene rappresentato da un vettore che giace nel piano dei due conduttori

La differenza di potenziale fra i due conduttori, di frequenza f, crea una corrente (corrente di spostamento) che scorre nell'isolante fra i due conduttori anch'essa con frequenza f; il complesso conduttori paralleli e dielettrico si comporta insomma come un condensatore.

Questa corrente di spostamento origina un campo magnetico H variabile con frequenza f che viene rappresentato da un vettore che giace su un piano perpendicolare a quello dei conduttori o, che è lo stesso, a quello su cui giace il vettore E.. (fig.7).

La presenza simultanea dei vettori E ed H fa si che si propaghi nello spazio la potenza fornita dal generatore sotto forma di un'onda elettromagnetica, di frequenza f (fig.7), in direzione perpendicolare al piano comune ad E e ad H.

La densità di questa potenza è pari a :

S = E x H (prodotto vettoriale).

Poiché E è  misurato in V/m , H in A/m ;  S, che rappresenta il vettore di Pointing, si misura in W/m². e rappresenta appunto la densità di potenza. dell'onda.

Il rapporto fra l'intensità del campo elettrico e quella del campo magnetico equivale all'impedenza caratteristica della linea ( in generale del mezzo in cui avviene la propagazione) ed è espressa in Ω.

Nelle linee il campo elettromagnetico si propaga nello spazio delimitato dai due conduttori.

Una caratteristica delle linee è la direzionalità di trasmissione , cioè l'onda si propaga nella direzione imposta dai conduttori senza dispersioni di potenza che non siano quelle dovute all'attenuazione della linea.

Quando le linee hanno una lunghezza minore di 1/4 della lunghezza d'onda  dei segnali che le percorrono sono considerate linee a bassa frequenza e vanno studiate seguendo la teoria delle costanti concentrate, se invece la loro lunghezza è uguale o maggiore di 1/4 della lunghezza d'onda dei segnali, si considerano ad alta frequenza e vanno studiate secondo la teoria delle costanti distribuite.

La  linea ad alta frequenza non si può dunque considerare come un solo elemento circuitale , come si fa con le linee a bassa frequenza (una semplice impedenza inserita in un punto fra generatore ed utilizzatore), ma va studiata col metodo delle costanti distribuite. , 

Nella applicazioni radio si incontrano evidentemente linee ad alta frequenza quali sono per esempio le linee di collegamento tra i trasmettitori e le antenne o tra le antenne ed i ricevitori.

Se in una  linea ad alta frequenza, dunque, viene applicato un segnale sinusoidale avente tensione V e corrente i è possibile descrivere il comportamento del quadripolo (una linea è un quadripolo con un segnale in ingresso ed uno, attenuato, in uscita)  mediante un sistema di equazioni differenziali con coefficienti r, l, g e c, chiamate costanti primarie, che sono:

• r : resistenza per unità di lunghezza dei conduttori;
• l : induttanza per unità di lunghezza della linea;
• g : conduttanza per unità di lunghezza dovuta al non perfetto isolamento fra i due conduttori della linea;
• c : capacità per unità di lunghezza .

Inoltre :

z₀ = r + jωl è l'impedenza per unità di lunghezza (RLC serie);

y₀ =  g + jωc è l'ammettenza  per unità di lunghezza (RLC parallelo). 

In fig. 9 è rappresentata schematicamente una linea ed indicate le equazioni differenziali.

i tipi di linee più utilizzati in radiotecnica sono le linee bifilari ed i cavi coassiali (fig.9). Le linee bifilari sono costituite da due conduttori paralleli distanti D separati da materiale dielettrico; esse hanno una impedenza caratteristica calcolabile con la formula  :

 

Z_c= (276/radq(ε_r))log(D/d)

dove  d è il diametro dei conduttori, D la distanza fra i conduttori ed ε_r la costante dielettrica relativa dell'isolante che separa i conduttori.

Per applicazioni con segnali ad alta frequenza questo tipo di linea presenta l'inconveniente di non essere protetta da disturbi elettrici esterni.

I cavi coassiali sono costituiti da un conduttore cilindrico sull'asse del quale è posizionato un'altro conduttore; i due conduttori sono separati dal dielettrico.

L'impedenza caratteristica si calcola con la formula:

Z_c= (138/radq(ε_r))log(D/d)

dove d è il diametro esterno del conduttore interno , D il diametro interno del conduttore esterno ε_r la costante dielettrica relativa del materiale interposto fra i due conduttori.

La propagazione dell'onda avviene nello spazio fra i due conduttori e risulta protetta dai rumori elettrici esterni.

Le onde S di fig.10 sono onde di superficie e si propagano a contatto più o meno continuo e diretto col suolo; le onde a, b, c sono onde di spazio ovvero onde fra due antenne in portata ottica.

Le onde S, a, b, c  costituiscono nel loro insieme l'onda diretta di terra.

L'attenuazione delle onde di superficie è elevata e l'intensità diminuisce notevolmente con la distanza e con la frequenza.

Ciò è dovuto al fatto che il suolo non è un perfetto dielettrico ma una via di mezzo fra conduttore e dielettrico.

Le onde a, b, c di fig. 10 sono onde di spazio il modo di propagarsi indicato in figura è quello tipico di antenna trasmittente ed antenna ricevente in portata ottica.

L'onda a arriva all'antenna ricevente con una determinata fase; l'onda b viene riflessa nel terreno , diventa c invertendo la fase ad arriva nell'antenna ricevente con fase opposta, o meglio la fase sarebbe esattamente opposta se la distanza a fosse uguale alla somma b + c. 

questo evidentemente non può verificarsi  e la somma b + c è sempre maggiore di a. Supponiamo che l'onda a sia di 300 mt e che  a-(b+c) = 5 mt.

l'onda  c arriva  con  5x360/300 = 6° di sfasamento che non compenserebbe lo sfasamento di 180° dato dalla riflessione.;  cioè in arrivo nell'antenna ricevente avrei:  fase di a -  sfasamento di c dovuto alla riflessione di b di 180° + 6° . Dunque l'onda  a rispetto all'onda c avrebbe una differenza difase altissima pari a 174° insomma non sentirei nulla.

Supponiamo ora che l'onda trasmessa sia di 10 mt e che la differenza di percorso sia sempre di 5 mt; in questo caso avrei sempre uno sfasamento dovuto alla riflessione pari a 180° , uno sfasamento dovuto alla differenza di percorso pari a 5x360/10= 180° che compenserebbe completamente il primo.

Insomma l'onda a e l'onda c arriverebbero nell'antenna ricevente in fase.

Da questo ragionamento risulta che l'onda di spazio da un contributo pressocchè nullo nelle trasmissioni a bassa frequenza ed un notevole contributo nelle trasmissioni ad alta frequenza.

per quanto riguarda le onde di spazio di fig.10 sembrerebbe che affinchè possa avvenire la comunicazione occorre che l'antenna trasmittente e quella ricevente siano a portata otticha che cioè la loro distanza sia minore o uguale d x 2 come si nota in figura 11.

d si ottiene dal seguente calcolo: 

(R+h)² - R² = d²  = R² +2Rh + h² -R² ; trascurando h² si ha:

d = radq(2Rh); poichè R=6.372.000 mt sia ha:

d= 3570 radq(h) ed  esprimendo h in mt e d in Km si ha: d=3,57 radq(h).

Se per esempio h= 5mt, per avere una portata ottica le due antenne dovrebbero distare 15,96 Km.

In realta però questa distanza è più grande ed è pari a 18,47 Km, come se le onde elettromagnetiche seguissero la curvatura della terra.

per calcolare d in pratica si usa quindi la formula  d= 4,13radq(h); è come se il raggio terrestre fosse non di 6.372Km  ma di  8.528Km.

Esistono delle condizioni della troposfera che permettono portate ben più ampie di quelle ottenibili con la normale onda di spazio, questo aumento della portata è dovuto alla rifrazione troposferica che varia in dipendenza delle condizioni atmosferiche; tali condizioni raramente rimangono stabili per lunghi periodi.

questa variazione (temporanea) di rifrazione troposferica determina un incurvamento delle onde elettromagnetiche, e quindi una maggiore portata,  che aumenta con l'aumento della frequenza e, di solito, dai 50 MHz in sù.

Il fenomeno si verifica di solito in prossimità del mare, d'estate, dopo il tramonto e prima dell'alba.

Da quanto finora detto si deduce che le trasmissioni ad alta frequenza sopra i 30 MHz avvengono principalmente con onda di terra (ad eccezione del traffico locale di breve distanza), sotto i 30 MHz avvengono con l'onda di cielo.

Sotto i 30 Mhz dunque le onde trasmesse giunte negli starti superiori dell'atmosfera vengono da questi riflesse sulla terra che le riflette a sua volta sull'atmosfera e così via; con successive riflessioni si possono coprire notevoli distanze di decine di migliaia di chilometri.

la riflessione delle onde dagli strati alti dell'atmosfera alla terra avviene  per la particolare conformazione dell'atmosfera.

L'atmosfera può considerarsi suddivisa in veri strati come mostrato in fig.12.

ai fini della propagazione delle onde di cielo  la ionosfera, che a sua volta è suddivisa in 4 sub-strati, e quello di  maggior interesse .

La ionizzazione della ionosfera è causata in massima parte dai raggi ultravioletti, intervengono nel fenomeno anche i raggi cosmici ed i raggi X,  essa presenta un andamento dapprima cresente poi, raggiunto un massimo, diminuisce. 

Questo andamento dipende dal fatto che i raggi ultravioletti incontrano un primo strato d'aria molto rarefatto e quindi la ionizzazione è limitata dai pochi atomi interessati, superato questo primo tratto incontrano uno strato più denso (gli atomi sono molto più numerosi) che si ionizza in misura maggiore del primo, ancora più in basso i raggi ultravioletti sebbene incontrino strati sempre più densi hanno perso molta della loro energia e creano  così una ionizzazione sempre minore.

E' evidente che la ionizzazione degli strati della ionosfera è un fenomeno molto complesso e dipende da vari fattori legati principalmente dalla potenza delle radiazioni emesse dal sole  che variano evidentemente in funzione posizione del sole rispetto alla terra, cioè nell'arco della giornata e  nell'arco dell'anno, in funzione della longitudine e della latitudine, ma  soprattutto in funzione dell'attività solare (cicli solari di 11 anni)..

La ionizzazione degli strati della ionosfera produce sostanzialmente due effetti:

• l'assorbimento dell'energia delle onde elettromagnetiche;
• la rifrazione e riflessione delle onde elettromagnetiche.

L'onda elettromagnetica trasmessa dall'antenna attraversa la troposfera e la stratosfera, non ionizzate, senza subire variazione di direzione,; arrivata alla ionosfera, che ha caratteristiche elettriche completamente differenti , non solo varia la propria velocità, ma varia anche la propria direzione.

Non viene però riflessa con un angolo acuto ma viene  dapprima  incurvata all'interno della ionosfere e poi riflessa sulla terra (fig.13)..

La curvatura che subisce l'onda dipende dal grado di ionizzazione dello starto interessato e dalla frequenza dell'onda incidente.

In particolare maggiore è la ionizzazione maggiore è la deviazione a parità di frequenza oppure per un determinato livello di ionizzazione la deviazione sarà maggiore, maggiore è la lunghezza d'onda.

In altri termini le onde lunghe si possono riflettere su strati a debole ionizzazione e le corte si riflettono sugli strati superiori della ionosfera a più alta ionizzazione.