fig.1

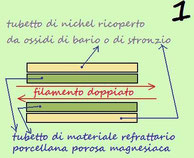
è posto un altro tubicino di materiale refrattario al cui interno è posizionato il filamento riscaldatore doppiato.
Il catodo a riscaldamento indiretto ha dimensioni maggiori rispetto all'altro tipo ed ha una notevole capacità termica che permette alla temperatura raggiunta dallo strato di ossidi di non pulsare sebbene siano alimentati a corrente alternata, così non capiterebbe per i catodi a riscaldamneto diretto se venissero alimentati a corrente alternata; La superficie di questi catodi risulta equipotenziale rispetto all'anodo diversamente da quanto accade nei filamenti ad accensione diretta fra le cui estremità vi è una d.d.p. Vf che si distribuisce in maniera uniforme lungo il filamento.
Il filo di riscaldamento dei catodi a riscaldamento indiretto viene doppiato per annullare il capo magnetico variabile determinato dalla corrente alternata di alimentazione.
Queste caratteristiche inflluiscono sull'emissione che risulta costante nei catodi a riscaldamento indiretto e variabile nell'altro tipo di catodo.


Emissione dovuta al riscaldamento.

Abbiamo già visto che con l'aumento della temperatura aumenta anche l'energia cinetica degli elettroni; affinchè un elettrone possa abbandonare il metallo per effetto della temperatura occorre che l'energia cinetica 1/2 m ₀ u² , con m ₀ massa dell'elettrone ed u la componente ortogonale alla superficie del metallo della velocità, sia maggiore del lavoro di estrazione che, come abbiamo già visto, è pari a V ₀.ε .
Prendiamo in considerazione il diodo di fig.2;

fig.2

se il catodo viene riscaldato, quando la sua temperatura è tale che l'energia cinetica di cui sopra eguaglia il lavoro di estrazione allora inizia l'emissione di elettroni dal catodo.
Questi elettroni se V di fig.2 è pari a zero si allontanano dalla superficie del catodo di qualche frazione di mm (circa 0,01 mm) e poi ricadono sul catodo medesimo.
Se invece V è maggiore di zero allora alcuni elettroni abbandonano il catodo e vengono attirati dall'anodo.
con l'aumento di V aumenta anche il numero di elettroni che raggiunge il catodo.

Esiste un valore di V_s per cui tutti gli elettroni emessi vengono raccolti dall'anodo; questo valore si chiama Potenziale di saturazione.
Gli elettroni che non giungono all'anodo permangono in prossimità del catodo e costituiscono una nube elettronia.
Ricapitolando possiamo dire che il numero massimo di elettroni che vengono emessi da catodo dipende dalla temperatura dello stesso e che il numero di elettroni che raggiungono l'anodo dipende dal valote della differenza di potenziale fra anodo e catodo.
Lo scienziato Richardson ha enunciato la seguente legge:

 Is = A.T². e .^(-b/T).S, dove I_s è la corrente di saturazione, in mA , A è una costante, T la temperatura assoluta , e la base dei logaritmi neperiani, ε la carica dell'elettrone in coulomb, S la superficie emmittente del catodo e b = V_o.ε /K tiene conto del lavoro di estrazione dell'elettrone con K costante di Boltzman.
Gli scienziati Langmuir e Child hanno enuciato la seguente legge : i = K . v ^3/2 che rappresenta l'andamento della corrente elettronica in funzione del potenziale di placca (anodo), K è una costante che dipende dalla geometria degli elettrodi.

fig.3

Servendoci di queste due leggi possiamo rappresentare graficamente la curva caratteristica del diodo di fig.3.
In realtà la caratteristica ha la forma tratteggiata in verde e questo perchè nelle leggi di Langmuir e Child si fanno delle ipotesi semplificative che non rispondono alla realtà .

fig.4

Osservando la fig. 4 Vediamo che di/dv rappresenta la conduttanza differenziale e la tangente nel punto viene anche detta pendenza della caratteristica; di solito per pendenza della caratteristica si prende quella relativa alla pendenza maggiore (tg β).
L'inverso della conduttanza differenziale è la resistenza differenziale dv/di ed ovviamente per resistenza del diodo si intende la resistenza differenziale minima.
Il compito del diodo è quello di raddrizzare una corrente alternata.

Se prendiamo in considerazione la fig.5 ci rendiamo conto che quando l'anodo è positivo gli elettroni vengono da lui attirati e si instaura una corrente i, quando invece l'anodo diventa negativo la corrente cessa.

fig.5

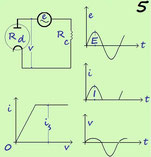
Nella fig.5  è rappresentato un circuito con un diodo  avente una curva caratteristica teorica con R_d = cost , dove  v =  R_d.i. 

Analizzando  il circuito possiamo scrivere che R _c.i = e - v, dove e = E.senω.t .

Possiamo anche osservare che quando e > 0 la resistenza  R_d del diodo è costante e quando e < 0, poichè non circola corrente,  R_d è infinita; si deduce allora che per e > 0 ,  i =  E.senω.t/( R+ R_d) =  v/ R_d e che per e < 0 ,  i = 0,  v = e

Cioè nei semiperiodi  positivi la corrente è sinusoidale , nei negativi è nulla e fra filamento e placca è applicata tutta la tensione con la placca negativa ; tale tensione è chiamata tensione invertita.

Vediamo ora qual'è l'espressione del rendimento del diodo.
Sappiamo che il rendimento η è uguale al rapporto fra la potenza utile P_u e la potenza di alimentazione P _a .
Considerando che P_a = e.i,  la potenza media di alimentazione  riferita ad un periodo è :
P _a= E/2.π ∫ ₀^2π i.senω.t d(ω.t)

fig.6

Considerando che  P _u= (e-v).i = R _c.i ² , la potenza media utile riferita a d un periodo è:

P _u= R _c/2.π ∫ ₀^2π  i² d(ω.t)

 sostituendo ad i la sua espressione:

 i=E.senω.t/(R_c+R_d) ,

sapendo che sen²ω.t=1/2 - 1/2 .cos2.ω.t e che la corrente i è nulla fra π e 2.π , si ottiene :
P_a=1/4.(E² /R_c+R_d) ;
P_u=1/4.(R_c.E²/(R_c+R_d)² .
Da queste espressioni si ricava:

η = P_u/P_a = R_c/(R_c+R_d) .
Nella fig.6 sono indicati due possibili schemi di utilizzazione dei diodi.
Lo schema a è impiegato nella maggior parte delle radio lo schema b è meno usato .