Circuito puramente resitivo
Consideriamo il circuito di fig.1a costituito da un generatore di tensione alternata e da un resistore.
L'espressione della corrente è: I = Imax.senωt ed ha l'andamento indicato in fig.1b; quella della tensione è per la legge di Ohm:
V = R.Imax.senωt ed ha l'andamento di fig.1c.
In queste espressioni Imax è pari a Ieff.√2.
La tensione e la corrente sono in fase come si evince dall'espressione analitica e si osserva in fig.1.
Circuito puramente induttivo
Consideriamo il circuito di fig.2a costituito da un generatore di tensione alternata e da una bobina (induttanza).
L'espressione della corrente è:
I = Ieff√2 senωt ed ha l'andamento indicato in fig.2b.
L'espressione della tensione è:
V = LdI/dt = L Ieff√2 ω cosωt.
Sapendo che cosωt = sen(ωt+π/2) l'espressione della tensione diventa:
V = L.Ieff√2 ω sen(ωt+π/2).
Ponendo Veff = L Ieff ω l'espressione di V diventa:
V = Veff √2 sen(ωt+π/2).
Confrontando l'espressione di V ottenuta con quella di I ci accorgiamo che la tensione è in anticipo rispetto alla corrente come si osserva anche nella fig.2c
Facendo il rapporto fra
Vmax = L.Ieff√2. ω e Imax = Ieff√2
ottengo la reattanza induttiva che risulta pari a :
Xl = ω L ;
facendo uso della notazione simbolica di ha :
Xl = Jω L ;
sempre in notazione simbolica la relazione fra reattanza induttiva tensione e corrente risulta:
V = Jω LI = XlI (vedi fig.2)
Circuito puramente capacitivo
Consideriamo ora il circuito di fig.3a costituito da un generatore di tensione alternata e da un condensatore (capacità).
L'espressione della tensione è:
V = Veff√2 senωt ed ha l'andamento indicato in fig.3b.
L'espressione della corrente è:
I = dq/dt; poichè q = CV ; I diventa uguale a:
I = CdV/dt = C.Veff√2 ω cosωt.
ponendo cosωt = sen(ωt+π/2) e C ω Veff = Ieff si ottiene:
I = Ieff√2 sen(ωt+π/2).
Confrontando l'espressione di I ottenuta con l'espressione di V ci accorgiamo che la tensione è in ritardo di π/2 rispetto alla corrente come si osserva anche nella fig.3c.
Facendo il rapporto fra Vmax = Veff√2. e Imax = C.ω.Veff√2 , ottengo la reattanza capacitiva che risulta pari a : Xc = 1/ω C ; facendo uso della notazione simbolica si ha: Xc = 1/Jω C ; sempre in notazione simbolica la relazione fra reattanza capacitiva tensione e corrente risulta:
V= I/Jω C = -JXcI (vedi fig.3)
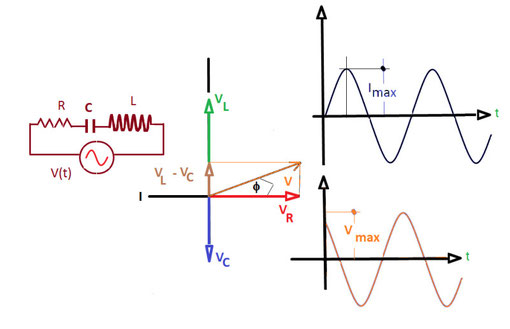
Circuito RLC serie
Consideriamo ora (fig.4) un circuito costituito da un resistore, una bobina (induttanza) ed da un condensatore (capacità) alimentati in SERIE da un generatore di tensione alternata.
Risulta:
V = √((VL-VC)2+VR2); Poichè da quanto precede risulta che
VL= I ω L e che
VC = I/ωC con semplici passaggi otteniamo:
V = I√((Lω-1/ωC)2 + R2).
L'espressione :
(√(Lω-1/ωC)2 + R2) rappresenta l'impedenza Z del circuito.
φ è l'angolo di fase (sfasamento fra tensione e corrente).
In notazione simbolica possiamo scrivere:
V = I (J(Lω-1/ωC) + R);
V/I = Z = R +J(ωL-1/ωC)
l'espressione ωL-1/ωC = X prende il nome di reattanza ed esattamente
ωL = XLè la reattanza induttiva e 1/ωC = XC è quella capacitiva.
X può essere positiva o negativa a seconda che prevalga l'induttanza o la capacità.
l'espressione di Z diventa : Z = R + JX e lo sfasamento φ diventa:
φ = arctgX/R.
L'inverso dell'impedenza Y = 1/Z prende il nome di ammettenza in SIEMENS
possiamo scrivere:
Y = 1/Z = 1/(R +J(ωL-1/ωC)) = 1/(R + JX) = (R-JX)/(R+JX)(R-JX)=
=(R-JX)/(R2+X2) =R/(R2+X2) -JX/(R2+X2) .
se poniamo :
- R/(R2+X2 ) = G che prende il nome di conduttanza in SIEMENS
- -X/(R2+X2) = B che prende il nome di suscettanza in SIEMENS
otteniamo : Y = G + JB
l'angolo di fase dell'ammettenza è uguale a -φ infatti esso è uguale a :
arctg B/G = -X/R questa espressione ci dice che l'angolo di fase dell'ammettenza è opposto a quello dell'impedenza cioè l'ammettenza capacitiva provoca uno sfasamento in anticipo della tensione rispetto alla corrente (φ positico) mentre l'ammettenza induttiva provoca uno sfasamento in ritardo della tensione rispetto alla corrente (φ negativo).

Se rappresentiamo l'impedenza Z e l'angolo di fase φ in funzione della frequenza otteniamo il diagramma di fig.5.
Per frequenze prossime a zero (corrente continua) il circuito è prevalentemente capacitivo , aumentando la frequenza fino al punto in cui XC = XL (risonanza) il circuito risulta puramente resistivo , infatti la capacità e l'induttanza si elidono a vicenda; aumentando ancora la frequenza il circuito diviene prevalentemente induttivo.
Nella fig. 5 è pure rappresentata la corrente che risulta massima in corrispondenza della frequenza di risonanza quando l'impedenza è minima.
La rappresentazione della corrente ci permettere di definire il concetto di selettività, cioè la caratteristica del circuito di farsi attraversare con facilità dalla corrente in condizioni di risonanza e di attenuare invece la corrente man mano che ci si allontana da tale condizione.
Nella rappresentazione della corrente di fig.5 abbiamo indicato il valore I0/√2 che è il valore di attenuazione per convenzione sopportabile; o meglio è il livello oltre il quale non ci si accorge della attenuazione; esso è pari al 70,71% del livello massimo ed anche pari ad una attenuazione di -3db; infatti 20 x log10(1/√2) è pari a -3.
a questa attenuazione corrispondono 2 valori di f: f1 ed f2 ; f1-f2 è pari alla larghezza di banda passante B.
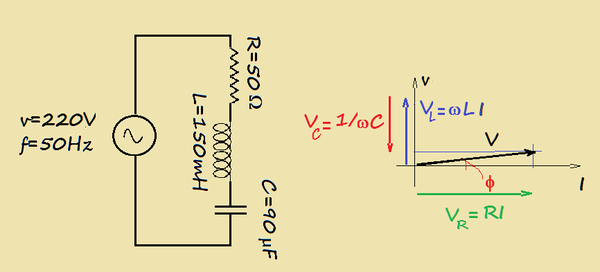
circuito RLC SERIE -esempio di calcolo
Dato il circuito RLC serie di fig.5a , conoscendo :
v = 220V, R = 50Ω, L = 150mH, C = 90μF, calcolare la tensione ai capi di R, L, C l'angolo di fase φ e disegnare il diagramma vettoriale.
Z = √(R2+(ωL-1/ωC)2) = 51,36 Ω
ωL= 47,12Ω
1/ωC= 35,37Ω
X=ωL-1/ωC= 11,75 Ω
in notazione simbolica si ha:
Z = R +JX = 50 + J11,75
φ = arctgX/R = 13°13'
la corrente che circola nel circuito è :
I = V/Z = 220/51,36 = 4,28A
la caduta su R è : 4,28 x 50 = 240V
la caduta su L è : 4,28 x 47,12 = 201,67V
la caduta su C è : 4,28 x 35,37 = 151,38V
per la costruzione grafica vedasi fig.5a
circuito RLC parallelo
Consideriamo ora (fig.6) un circuito costituito da un resistore, una bobina (induttanza) e da un condensatore (capacità) alimentati in PARALLELO da un generatore di tensione alternata.
Risulta:
I=radq((IC-IL)2+IR2); Poichè sappiamo che IL=V/ωL, che IC=VωC e che IR=V/R, con semplici passaggi otteniamo:
I=V √((ω.C-1/ω.L)2+1/R2); da questa espressione si ricava l'Impedenza del circuito:
Z= 1/√(1/R2 + (ωC - 1/ω.L)2 );
φ è l'angolo di fase (sfasamento fra tensione e corrente).
L'inverso dell'impedenza 1/Z= Y risulta:
Y = √(1/R2 + (ωC-1/ωL)2)
che in notazione simbolica diventa:
Y = 1/R+ J(ωC-1/ωL)
In questa espressione 1/R e la conduttanza in SIEMENS, ωC la suscettanza capacitiva in SIEMENS e 1/ωL la suscettanza induttiva in SIEMENS.

Se rappresentiamo l'impedenza Z e l'angolo di fase φ in funzione della frequenza otteniamo il diagramma di fig.7.
Per frequenze prossime a zero (corrente continua) il circuito è prevalentemente Induttivo , aumentando la frequenza fino al punto in cui XC=XL (risonanza) il circuito risulta puramente resistivo , infatti la capacità e l'induttanza si elidono a vicenda; aumentando ancora la frequenza il circuito diviene prevalentemente capacitivo.
Nella fig. 7 è pure rappresentata la tensione che risulta massima in corrispondenza della frequenza di risonanza quando l'impedenza è massima.
La rappresentazione della tensione ci permettere di definire il concetto di selettività, cioè la caratteristica del circuito di mantenere ai suoi capi una tensione elevata in condizioni di risonanza e di attenuare invece la tensione man mano che ci si allontana da tale condizione.
Nella rappresentazione della tensione di fig.7 abbiamo indicato il valorre V0/√2 che è il valore di attenuazione per convenzione sopportabile; o meglio è il livello oltre il quale non ci si accorge della attenuazione; esso è pari al 70,71% del livello massimo ed anche pari ad una attenuazione di -3db; infatti 20 x log10(1/√2) è pari a -3.
a questa attenuazione corrispondono 2 valori di f: f1 ed f2 ; f1-f2 è pari alla larghezza di banda passante B.
circuito RLC PARALLELO -esempio di calcolo
Dato il circuito RLC parallelo di fig.7a , conoscendo :
v = 220V, R = 50Ω, L = 150mH, C = 90μF, calcolare le correnti IR, IL, IC, l'angolo di fase φ e disegnare il diagramma vettoriale.
Y = √(1/R2+(ωC-1/ωL)2) = 0,0212 S
ωC = 0,028 S
1/ωL = 0,021 S
in notazione simbolica si ha:
Y = 1/R + J(ωC-1/ωL) = 0,02 + J1(0,028-0,021) = 0,02 + J 0,007;
0,02 è la conduttanza G , 0,007 è la suscettanza B.
φ = arctg(ωC-1/ωL)/(1/R) = 19°17'
per quanto riguarda le correnti possiamo scrivere:
IR = v x 1/R = 4,4 A
IC = v x ωC = 6,16 A
IL = v x 1/ωL = 4,62 A
la corrente totale è pari a :
I = v x Y = 220 x 0,0212 = 4,66A
per la costruzione grafica vedasi fig.5a
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta