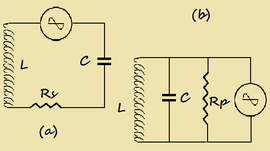
In regime di oscillazioni forzate il periodo non dipende dalle costanti del circuito ma dalle caratteristiche della sorgente di alimentazione che può essere in serie (fig.1a) o in parallelo (fig.1b).

Con l'alimentazione in serie tutti gli elementi del circuito sono percorsi dalla stessa corrente, con quella in parallelo sono sottoposti alla stessa tensione.

I due schemi sono la rappresentazione di un medesimo circuito  , sono cioè equivalenti,  purchè L e C siano le stesse del circuito reale  ed R_s ed R_p diano origine alla medesima perdita di energia che si manifesta nello stesso.

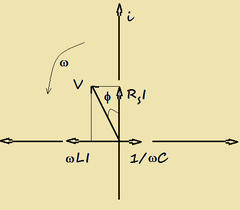
In fig.2 è mostrato il diagramma vettoriale del circuito alimentato in serie da cui si ricava:

V²=R_s²I² + I²(ωL - 1/ωC)²

da cui :

V=I radq(R_s² + (ωL - 1/ωC)² );

Z_s= V/I= radq(R_s² + (ωL - 1/ωC)²). 

Dall'espressione dell' Impedenza Z_s si ricava che se ωL-1/ωC = 0  allora Z è minima e la corrente è massima , come si nota in fig.3.

Quindi fissati L e C avrò una corrente massima nel circuito quando ω = ω₀

 è tale da soddisfare l'espressione su indicata.

da questa espressione si ricava il valore della frequenza che per quei valori di L e C rende massima la corrente:

f₀= 1/2π(radq(LC)).

Siamo nelle condizioni di risonanza quando la tensione ai capi dell'induttanza (ωLI) é uguale e contraria a quella  ai capi del condensatore (I/ωC).

Se dividiamo tale tensione per quella di alimentazione che in risonanza è uguale a R_sI otteniamo il coefficiente di risonanza  ε= ω₀L/R_s = 1/ω₀CR_s .

Nella fig.3 è indicata la curva di risonanza del circuito.

Quando l'impedenza è minima la corrente è massima; in condizioni di risonanza l'impedenza Zs è uguale a Rs.

In fig.4 è mostrato il diagramma vettoriale del circuito alimentato in parallelo da cui si ricava:

I²=V²/R_p²+ V²(ωC - 1/ωL)²

da cui :

I=V radq(1/R_p² + (ωC - 1/ωL)²;

1/Z_p= Y_p= I/V= radq(1/R_p² + (ωC - 1/ωL)².

Dall'espressione dell' ammetenza Y_p si ricava che se ωC-1/ωL = 0  allora Y_p è minima e la tensione è massima .

Quindi fissati L e C avrò una tensione  massima nel circuito quando ω = ω₀ è tale da soddisfare l'espressione su indicata.

da questa espressione si ricava il valore della frequenza che per quei valori di L e C rende massima la tensione:

f₀= 1/2π(radq(LC)) , espressione identica a quella trovata per il circuito alimentato in serie.

  Siamo nelle condizioni di risonanza quando la corrente che attraversa l'induttanza (V/ωL) é uguale e contraria a quella  che attraversa il condensatore (ωCV).

Se dividiamo tale corrente  per quella di alimentazione che in risonanza è uguale a V/R_p otteniamo il coefficiente di risonanza  ε= ω₀CR_p = R_p/ω₀L.

Nella fig.5 è indicata la curva di risonanza del circuito.

Quando l' Ammetenza  è minima la tensione è massima; in condizioni di risonanza l'Ammetenza Y_p è uguale a 1/R_p.