Bobine di TESLA
Nikola Tesla, è stato un fisico, inventore e ingegnere serbo -croato che operò negli Stati Uniti d'America.
È conosciuto soprattutto pere i suoi numerosi contributi nel campo dell’elettromagnetismo.
E’ vissuto fra la fine dell’Ottocento e gli inizi del Novecento. I suoi brevetti e il suo lavoro formano la base del moderno sistema elettrico a corrente alternata .
Tesla condusse innovativi esperimenti sulla luce elettrica, fenomeni di corrente alternata ad alta frequenza e trasmissione di segnali e di energia elettrica senza fili.
TESLA era un genio assoluto, tutto quello che ha inventato e brevettato ha sempre funzionato alla perfezione e non aveva bisogno di progettare nella carta alcunché; tutte le sue invenzioni passavano dal suo cervello , " pitticcu su ciorbeddu !!! " , alla realizzazione pratica.
Ho letto da qualche parte che stava per regalarci l'energia gratuita, ed oggi ce ne fotteremo delle enormi spese che affrontiamo per l'energia che ci è necessaria se non fosse che i grandi " MERDE " capitalisti che avrebbero dovuto finanziarlo l'hanno, invece, affossato " good bye Tesla "; "pezzi di merda cagati a forza."......... certo, che cazzo avrebbero succhiato da un progetto che avrebbe portato ad una energia gratuita? Purtroppo viviamo in una società governata da questi stronzi che in ultima analisi però, a ben pensarci, poveretti, stanno peggio degli altri, pare infatti che mentre pensano a far soldi, incamerino un notevole numero di corna.
E' Vergognoso, la scuola pubblica ha ignorato un genio di tale grandezza.
Chi infatti ricorda qualche testo scolastico di materie scientifiche che lo menzioni? forse, ma non ne sono certo, gli è stata dedicata qualche riga..
Ancora oggi, quando si sente parlare di Tesla, alla maggior parte delle persone interessate ad argomenti scientifici, viene in mente solo la " Bobina di Tesla " .
Ma cosa è la bobina di TESLA.................ah...................."....è quella che produce scariche elettriche simili a dei mini fulmini e se ci metti vicino un tubo al neon " ...questo si illumina".........
In effetti ho scopiazzato qualche circuito con la bobina di tesla, su internet se ne trovano un fottio, e le lampade al neon si sono accese.............e ho notato pure delle scariche .....................................a questo punto mi son detto ma come tubo funziona questa benedetta bobina di Tesla? e sopratutto a cosa serve? solo per accendere tubi al neon o produrre fulmini artificiali?
Che i tubi al neon si accendono è dovuto al fatto che avvicinandoli in un campo magnetico variabile ad alta frequenza ( da qualche decina a qualche migliaio di Kh) il neon si ionizza, cioè gli atomi assorbono energia tale da perdere degli elettroni che poi ritornando al loro posto la restituiscono emettendo luce (fotoni).
Che producano fulmini dipende dall'altissimo valore della tensione raggiunta dal secondario.
Per quando riguarda le bobine di Tesla o pseudo tali, le varie teorie a corredo degli schemi trovati su internet dicono probabilmente delle cose giuste ma non spiegano assolutamente nulla di nulla ..................insomma non sapevo nulla delle bobine di Tesla ed ora, dopo aver vagato su internet, né so ancora di meno.
Insomma come disse Garibaldi " intrendi in Roma in su tempu de sa carruba " , , le idee sono poche ma ben confuse..
Su internet leggi :
- ................ la bobina di Tesla è un tipo di trasformatore risonante che consiste in due circuiti elettrici accoppiati risonanti;
- .........................un trasformatore a bobina di Tesla opera in modo diverso dal trasformatore convenzionale, in cui il guadagno di tensione è limitato al rapporto dei numeri di giri delle spire. Diversamente, il guadagno di tensione di una bobina di Tesla può essere molto più grande;
- .......................il guadagno in tensione è pari ( ? ) alla radice quadrata del rapporto fra l'induttanza del secondario e quella del primario o fra la capacità del primario e quella del secondario ;
- ..........................la bobina trasferisce energia da un circuito primario risonante ad un secondario che oscilla alla stessa frequenza.
- ..................la tensione del secondario aumenta finché tutta l’energia primaria è stata trasferita .
Relativamente alle affermazioni di cui ai punti 1, 2, 4, 5 nulla da obbiettare ma ciò che viene detto al punto 3 mi pare incomprensibile ..................osservo infatti che se considero un trasformatore di Tesla come un normale trasformatore l'incremento di tensione dovrebbe essere pari al rapporto fra le spire del secondario e quelle del primario,
Se considero invece questo acrocco come un trasformatore di Tesla l'incremento della tensione dovrebbe essere molto maggiore ( è questo è vero , all'estremità del secondario si generano infatti dei fulmini) e pari alla radice quadrata del rapporto fra l'induttanza del secondario e quella del primario, e questo mi pare falso, infatti, se facciamo questo raffronto la bobina di Tesla ne esce perdente.
infatti l'induttanza del primario è dell'ordine delle decine di micro henry , quella del secondario dell'ordine delle migliaia di micro henry , la radice quadrata del loro rapporto è dell'ordine delle poche decine .
Il rapporto delle spire del secondario rispetto a quelle del primario viceversa è dell'ordine di molte decine.
DOVE SBAGLIO ?
l'affermazione di cui al punto 3 deriva dalla affermazione di cui al punto 5; infatti poiché l'energia del primario che è pari a :
- Ep= 1/2 C1V12
e quella del secondario è pari a:
- Es= 1/2 C2V22 ,
se tutta l'energia del primario è stata trasferita al secondario sarà Ep = Es e quindi
sarà:
- V2 = V1 √(C1/C2)
ricordando poi che in risonanza è 2πfL= 1/2πfC sarà anche:
- V2 = V1√(C1/C2) = V1 √(L2/L1)
Ora, poiché in un trasformatore ad induzione il guadagno è pari a:
L2/L1 infatti V2 = V1 (L2/L2) , ancora una volta vien fuori che a parità di induttanze il guadagno in un trasformatore ad induzione è
maggiore di quello di un trasformatore di Tesla (a risonanza)..
In realtà secondo me un paragone fra un trasformatore tradizionale (ad induzione) ed un trasformatore di Tesla (a risonanza) non ha senso, sono due cose diverse.
- il trasformatore ad induzione ha un coefficiente di accoppiamento circa uguale a 1;
- il trasformatore ad induzione ha un coefficiente di accoppiamento variabile fra 0,05 e 0,2 ;
-
ll trasformatore ad induzione ha un nucleo magnetico;
- l trasformatore di Tesla (a risonanza) è avvolto in aria;
- gli avvolgimenti di un trasformatore ad induzione non hanno condensatori; ( se li hanno non hanno influenza sul guadagno di tensione );
- gli avvolgimenti del trasformatore a risonanza hanno i condensatori ( i due avvolgimenti coi condensatori costituiscono due circuiti LC con un basso coefficiente di accoppiamento e risonanti).
Insomma sono due cose diverse.
E' un fatto però che la tensione che si può ottenere al secondario di un trasformatore di Tesla è molto alta; il guadagno è molto più alto di quello dato dal rapporto fra le spire del secondario e quelle del primario.
Ciò è dovuto al fatto che se il primario (circuito LC) ha una frequenza pari a quella del secondario (anch'esso circuito (LC)), la tensione al secondario diviene molto grande.
Perché avviene questo?

Per capirlo prendiamo il circuito LC di fig.1.
Applicando la legge di Kirchoff otteniamo l'espressione di Vg(t) indicata in fig.1 .
Il nostro problema è quello di risolvere questa equazione differenziale non omogenea.
Per far questo operiamo in questo modo:
Prendiamo l'equazione omogenea ad essa associata :
- Ld2Q/dt2 + Q(t)/C = 0
La soluzione di questa equazione la conosciamo ed è pari a:
Q(t)= Q0 cos(ωt) da cui essendo VC = Q sarà :
V(t)= V0 cos(ωt) (vedi circuiti oscillatori -oscillazioni libere).
poichè i= dQ(t) sarà : i(t)= -Q0ω sen(ωt)
Prendiamo ora l'equazione non omogenea:
- Ld2Q/dt2 + Q(t)/C = Vgen
Poniamo Vgen = V0 sen(Ωt) con Ω diverso da ω = 1/√LC.
L'equazione differenziale non omogenea diventa:
Ld2Q(t)/dt2 + Q(t)/C = V0 sen(Ωt); (in questa equazione compare Ω ed ω infatti Q(t) = Q0 cos(ωt) )
La soluzione è del tipo: Q = Asen(Ωt) ; calcoliamo la derivata seconda e poniamola nella equazione non omogenea:
dQ2/dt2 = -AΩ2sen(Ωt) ponendo questo valore di Q nella equazione non omogenea abbiamo:
-LAΩ2sen(Ωt) + A sen(Ωt)/C = V0 sen(Ωt) ; dividendo per Lsen(Ωt) otteniamo:
-AΩ2 + A /LC = V0/L poiché 1/LC è uguale a ω2 si ottiene:
-AΩ2 + A ω2 = V0/L da cui A=V0/L (ω2-Ω2 ) in fine si ottiene:
Q = V0sen(Ωt)/L (ω2-Ω2 ).
A questo punto aggiungendo questa soluzione a quella della equazione omogenea associata otteniamo il risultato cercato :
Q(t) =Q0cos(ωt) - V0sen(Ωt)/L (ω2-Ω2 ).
V(t) =V0cos(ωt) - V0sen(Ωt)/CL (ω2-Ω2)
I(t) = - Q0ωsen(ωt) + V0Ωcos(Ωt)/L (ω2-Ω2 )
Ci rendiamo conto che le oscillazioni hanno un'ampiezza aumentata dal secondo termine aggiuntivo ma raggiunge un valore limitato; questa soluzione infatti non mi dice se e quanto il secondo termine cresce col tempo
Vediamo inoltre che se e ω e Ω sono molto diversi il secondo termine è trascurabile.
Se invece risolviamo l'equazione differenziale
Ld2Q(t)/dt2 + Q(t)/C = V0 sen(Ωt)
ponendo Ω = ω otteniamo la seguente soluzione:
Q(t) =Q0cos(ωt) - V0tcos(ωt)/2Lω
V(t) =V0cos(ωt) - V0tcos(ωt)/2CL ω
I(t) = - Q0ωsen(ωt) + V0tωsen(ωt)/2L ω
Osserviamo che l'ampiezza della corrente e della tensione aumenta col tempo cresce cioè ad ogni ciclo e tende all'infinito per t che tende all'infinito.
come si ottiene questa soluzione?
intanto scriviamo l'equazione Ld2Q(t)/dt2 + Q(t)/C = V0 sen(ωt),
dividendo per L otteniamo: d2Q(t)/dt2 + Q(t)/LC = V0 sen(ωt)/L ;
la nostra equazione può essere scritta:
d2Q(t)/dt2 + ω2Q = (V0/2LJ )( eJ ωt - e -J ωt )
la soluzione è del tipo :
Q(t) = (A + Bt)e kt dove k = ± Jω;
l'espressione può essere scritta:
Q(t)= A e kt + Bte kt
la derivata seconda di questa espressione vale:
derivata prima:
AKe kt + BtKe kt + Be kt
derivata seconda:
AK2e kt + BtK2e kt+ BKe kt + BKe kt =
e kt(AK2 + BtK2+ BK + BK) = e kt (K2 ( A+Bt) t 2 BK ) = d2Q(t)/dt2
sostituendo l'espressione della derivata seconda nell'equazione rossa otteniamo:
e kt (K2 ( A+Bt) t 2 BK )+ ω2 (A + Bt)e kt = (V0/2LJ )( eJ ωt - e -J ωt )=
e kt ((K2 + ω2 )(A+Bt) t 2 BK ) = (V0/2LJ )( eJ ωt - e -J ωt )
dobbiamo ora calcolare A e B ed inserirli nell'equazione verde.
Per k = + Jω abbiamo:
eJ ωt ((-ω2+ ω2 )(A++B+t) t 2 B+Jω ) = (V0/2LJ )
eJ ωt ;
2 B+Jωe kt= (V0/2LJ )
eJ ωt
2 B+Jω = (V0/2LJ ) ; B+= -V0/4Lω.
Per k = - Jω abbiamo:
e -Jωt ((-ω2+ ω2 )(A-+B-t) - 2 B-Jω ) = -(V0/2LJ )e-J ωt ;
- 2 B-Jωe -Jωt= -(V0/2LJ ) e -J ωt ;
-2 B-Jω = -(V0/2LJ ) ; B-= -V0/4Lω.
risulta A+ = A- = 0 e B+ = B- = B quindi otteniamo:
B= -V0/4Lω. dobbiamo inserire questo valore nella equazione verde .
l'equazione Q(t) = (A + Bt)e kt dove k = ± Jω può essere scritta:
Q(t) = BteJ ωt + Bte-J ωt = Bt(eJ ωt + e-J ωt ) =
= V0t/4LJ2ω.(eJ ωt + e-J ωt ) = (-V0t/2Lω).(cos ωt)
questa soluzione va aggiunta alla soluzione della equazione omogenea associata ed alla fine si ottiene:
Q(t) =Q0cos(ωt) - V0tcos(ωt)/2Lω
V(t) =V0cos(ωt) - V0tcos(ωt)/2CL ω
I(t) = - Q0ωsen(ωt) + V0tωsen(ωt)/2L ω c.v.d.
Dopo tutte queste benedette formule (si può consultare : "La bobine de Tesla" di Christopher Gerekos dell'Università di Bruxelles) che ci dicono come cresce la tensione, vediamo la fig.2.
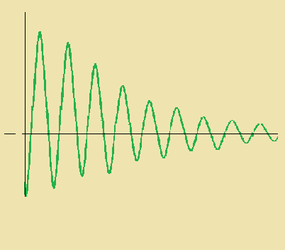
La fig.2A più la fig.2B rappresentano il trasformatore di TESLA. la parte A , quando il condensatore si è caricato e lo spinterometro ha chiuso il circuito, rappresenta un circuito che oscilla ad una frequenza pari a 1/2π√(LC); la velocità angolare è ω = 1/√(LC) . L'oscillazione è smorzata ed è rappresentata in fig.3 , si ottiene risolvendo l'equazione differenziale omogenea di cui prima abbiamo parlato.
Questa tensione per induzione si trasmette nel secondario il quale è come se avesse in serie un generatore, come rappresentato in fig.2C, ed inizia ad oscillare alla stessa frequenza; perché questo avvenga ovviamente è necessario che L1 C1 sia uguale a L2 C2 , che il primario ed il secondario cioè siano in risonanza e quindi sia l' ω del primario uguale all'ω del secondario.

il secondario di fig.2C può essere rappresentato come in fig.2D.
E' esattamente il circuito che abbiamo studiato con un generatore che fornisce una tensione Vgen = Ld2Q/dt2 + Q(t)/C. la V(t)di questa equazione differenziale non omogenea , quando la velocità angolare relativa al generatore e quella relativa all'oscillazione del secondario sono uguali , è quella appena studiata, e cioè:
V(t) =V0cos(ωt) - V0tcos(ωt)/2CL ω ed ha l'andamento riportato in fig.4.
Ricapitolando ecco come funziona il trasformatore di TESLA.
- Si accende il generatore del primario;
- lo spinterometro è aperto,;
- il generatore carica il condensatore del primario;
- quando il condensatore è carico si accende lo spinterometro ed il generatore viene escluso. (abbiamo un circuito LC omogeneo);
- il circuito LC oscilla alla sua frequenza di risonanza f = 1/2π radq(LC);
- Le oscillazioni del primario generano per induzione una f.e.m. nel secondario. dove LsCs=LpCp
- le oscillazioni del primario sono smorzate ; i man mano che queste diminuiscono aumentano quelle indotte nel secondario.(fig. 5).
- Le oscillazioni del primario si comportano come un generatore di tensione alternata per il secondario.
- il secondario dunque va considerato come un circuito LC non omogeneo.
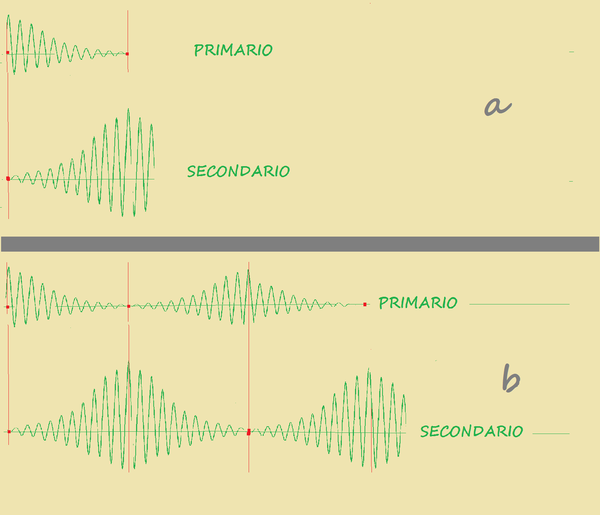
In fig.5 sono mostrate le forme delle oscillazioni nel primario e nel secondario
in fig.5a lo spinterometro si spegna al primo nodo, dopo di che il ciclo si ripete.
in fig.5b lo spinterometro si spegna al secondo nodo ; potrebbe spegnersi anche al 3° 4°............. nodo dopo di che il ciclo si ripete; l0 spegnimento dello spinterometro e quindi la ripetizione del ciclo dipende dal coefficiente di accoppiamento.
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta