Prendiamo sempre in considerazione un NPN , il discorso sul  PNP non cambia.

Siamo in zona attiva diretta; trattandosi di piccolo segnale l'operazione che vogliamo fare è infatti quella di amplificarlo.

in Corrente continua si è trovato il punto di riposo Q ed ora il piccolo segnale varia intorno a questo punto.

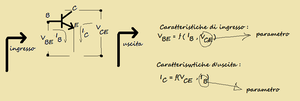
In fig.1 è disegnato un PNP in configurazione ad emettitore comune ; in fig.2  sono indicate .le caratteristiche d'ingresso e d'uscita .

 

Le caratteristiche sono :

 

1. caratteristica d'uscita indicata nella fig.2 a sinistra.
2. la caratteristica d'ingresso indicata in fig.2 a destra.

 

vediamo l'espansione al primo ordine delle caratteristiche d'uscita:

Intorno al punto Q ho:

I_C + i_C = i_C (V_CEQ + v_CE , I_BQ +i_B) facendo l'espansione al primo ordine abbiamo:

I_CQ + i_C = i_C (V_CEQ, I_BQ) + (δ i_C /δ v_CE )v_CE + (δ i_C /δ _iB )i_B

Le derivate parziali sono fatte intorno al punto Q.

I termini rossi sono uguali e si elidono ; rimane allora:

 i_C =  (δ i_C /δ v_CE )v_CE + (δ i_C /δ _iB )i_B

_{se pongo} (δ i_C /δ v_CE ) = h_oe e  (δ i_C /δ _iB )=  h_fe   , ottengo:

 

 

  i_C =  h_oev_CE + h_fe i_B

 

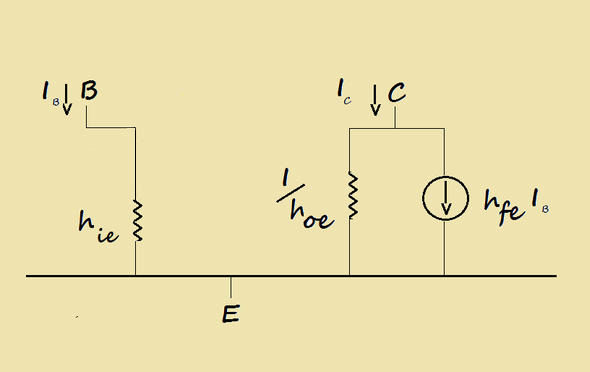
l'espressione rappresenta la linearizzazione delle caratteristiche d'uscita del transistore in configurazione CE (comon emitter).

In figura 3 è rappresentato il modello di tale espressione.

Essendo i_C la somma di due correnti il modello non può che essere costituito da due elementi in parallelo.

 

Vediamo ora l'espansione al primo ordine delle caratteristiche di ingresso raffigurate nella parte destra di fig.2

Nell'intorno del punto Q posso scrivere:

V_BE + v_BE =V_BE (I_BQ + i_B , V_CEQ + v_CE) facendo l'espansione al primo ordine abbiamo:

V_BE + v_BE = v_BE (I_BQ, V_CEQ) + (δ v_BE /δ i_B )i_B + (δ v_BE /δ v_CE ) v_CE

Le derivate parziali sono fatte intorno al punto Q.

I termini rossi sono uguali e si elidono ; rimane allora:

v_BE = (δ v_BE /δ i_B )i_B + (δ v_BE /δ v_CE ) v_CE   

se pongo  (δ v_BE /δ i_B ) = h_ie e  (δ v_BE /δ v_CE ) =  h_re   , ottengo

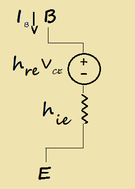
v_BE = h_ie i_B + h_re  v_CE

 

l'espressione rappresenta la linearizzazione delle caratteristiche di ingresso del transistore in configurazione CE (comon emitter). In figura 4 è rappresentato il modello di tale espressione.

Essendo v_BE la somma di due tensioni il modello non può che essere costituito da due elementi in serie.

 

 

 

oltre che analiticamente h_fe può essere determinato anche graficamente utilizzando le caratteristiche di uscita come si nota in fig.6

 

 

 

 

l'espessione di h_oe è:

 

h_oe= δ i_C /δ _vCE

 

Osservando le caratteristiche d'uscita di fig.7 vediamo che  h_oe altro non è che la pendenza della retta i_BQ. (in figura la pendenza è stata accentuata)

l'espessione di hie è:

 

h_ie= δ v_BE /δ i_B

 

 

 

Osservando le caratteristiche d' ingresso di fig.8 vediamo che h_ie altro non è che la pendenza della curva v_CE che contiene il punto di riposo (lavoro) Q.

Graficamente posso approssimare il valore di h_ie  con l'espressione :

h_ie=  (v_BE2-v_BE1)/(I_B2-I_B1)

 

Utilizzando il modello di EBERS e MOLL ottengo per via analitica la seguente espressione:  h_ie = v_T β_ie / I_C

In realtà nel transistor esiste anche una resistenza fra B,' che è la base del transistore intrinseco, e B che è il contatto esterno della base del transistore reale (esistono anche le resistenze simili relative all'emettitore e al collettore ma sono trascurabili).

Esistono anche due condensatori; uno fra B' ed E chiamato C B'E oppure Cπ ed uno, di capacità inferiore (si ricordi infatti che la giunzione B'C è polarizzata inversamente) fra B' e C chiamata CB'C oppore Cμ.

Un certo GIACOLETTO ha tenuto conto di questa resistenza e di questi condensatori e ha teorizzato un nuovo modello disegnato in fig.8c.

 

 

Con le basse e medie frequenze il modello di fig.5 può essere semplificato come in fig.9

in quiell'ambito infatti i parametri  h_re e h_oe possono essere trascurati.

Nella configurazione a base comune, rappresentata in fig.11, il segnale viene immesso fra emettitore e massa tramite il condensatore C₃ e viene prelevato fra collettore e massa tramite il condensatore C₂.

La base , comune all'emettitore ed al collettore, , ai fini del segnale, è collegata a massa tramite il condensatore C₁.

Possiamo analizzare il circuito di fig.15a dal punto di vista statico (analisi di grande segnale) e dal punto di vista dinamico o ANALISI DI PICCOLO SEGNALE.

 

PUNTO DI VISTA STATICO

Nell'analisi statica si considera il circuito alimentato dalla sola corrente continua; il segnale è assente.

Nel circuito i condensatore è come se costituissero dei circuiti aperti.

il circuito di fig11a diventa pertanto come quello di fig.11b e quindi di fig.11c.

Considerando la fig.11c , possiamo scrivere:

V_B = V_cc(R₂/R₁+R₂); considerando che V_BE = 0,7V  possiamo inoltre scrivere:

V_E = V_B-0,7 = V_cc(R₂/R₁+R₂) - 0,7 ; e inoltre :

V_C = V_cc-R_cI_c

 

PUNTO DI VISTA DINAMICO-

ANALISI DI PICCOLO SEGNALE

 

Per fare l'analisi dinamica utilizziamo il modello semplificato di fig.8a. .

I 2 condensatori di accoppiamento  ed il condensatore di bypass dello schema di fig. 12 costituiscono dei circuiti aperti per la corrente continua e dei corto circuiti per la corrente alternata alla frequenza del segnale che vogliamo amplificare.

 

Operiamo a centro banda,  cioè in quell'intervallo di frequenze in cui l'amplificazione non dipende dalla frequenza.

 

Nel circuito non ci sono cioè elementi reattivi;  il circuito è solo resistivo. 

Inoltre i generatori di corrente continua e di tensione continua costituiscono anch'essi dei corto circuiti per il segnale. 

Sotto queste ipotesi possiamo , nel caso di fig.12 , eliminare  i condensatori e considerare il generatore di tensione continua , massa per il segnale.

 

 

 

 

Per lo schema indicato a destra in alto nella fig.12 possiamo utilizzare il modello di sinistra in alto tratto dalla fig.8a.

Il calcolo dell'amplificazione di corrente e di tensione è indicato in fig.12.

 

I valori ottenuti dipendono anche  dal carico (altoparlante), da elementi cioè esterni all'amplificatore e ciò ci impedisce di fare un raffronto fra vari amplificatori.

 

 

 

Per permettere il raffronto possiamo calcolare l'amplificazione intrinseca a vuoto che dipende unicamente da elementi interni all'amplificatore. Il calcolo dell'amplificazione intrinseca a vuoto è indicato in fig.13.

Nella fig.14 e nella fig.15  sono riportati i calcoli della resistenza di ingresso e della resistenza di uscita dell'amplificatore in configurazione a base comune.

Nella configurazione ad emettitore  comune, rappresentata in fig.16, il segnale viene immesso fra base e massa tramite il condensatore C₁ e viene prelevato fra collettore e massa tramite il condensatore C₂.

L'emettitore , comune alla base ed al collettore, , ai fini del segnale, è collegata a massa tramite il condensatore C₃.

Possiamo analizzare il circuito di fig.17a dal punto di vista statico e dal punto di vista dinamico.

PUNTO DI VISTA STATICO

Nell'analisi statica si considera il circuito alimentato dalla sola corrente continua; il segnale è assente.

Nel circuito i condensatore è come se costituissero dei circuiti aperti.

il circuito di fig16a diventa pertanto come quello di fig.16b e quindi di fig.16c.

Considerando la fig.16c. , possiamo scrivere:

V_B = V_cc(R₂/R₁+R₂); considerando che V_BE = 0,7V  possiamo inoltre scrivere:

V_E = V_B-0,7 = V_cc(R₂/R₁+R₂) - 0,7 ; e inoltre :

V_C = V_cc-R_cI_c

 

 

PUNTO DI VISTA DINAMICO-

 

ANALISI DI PICCOLO SEGNALE

 

 

Per fare l'analisi dinamica utilizziamo il modello semplificato di fig.8a. .

I 2 condensatori di accoppiamento  ed il condensatore di bypass dello schema di fig. 17a costituiscono dei circuiti aperti per la corrente continua e dei corto circuiti per la corrente alternata alla frequenza del segnale che vogliamo amplificare.

Operiamo a centro banda, cioè in quell'intervallo di frequenze in cui l'amplificazione non dipende dalla frequenza. Nel circuito non ci sono cioè elementi reattivi; il circuito è solo resistivo. Inoltre i generatori di corrente continua e di tensione continua costituiscono anch'essi dei corto circuiti per il segnale. Sotto queste ipotesi possiamo , nel caso di fig.17a , eliminare i condensatori e considerare il generatore di tensione continua , massa per il segnale.

 

Per lo schema indicato a destra in alto nella fig.17a possiamo utilizzare il modello di sinistra in alto tratto dalla fig.8a. Il calcolo dell'amplificazione di corrente e di tensione è indicato in fig.17a I valori ottenuti dipendono anche dal carico (altoparlante), da elementi cioè esterni all'amplificatore e ciò ci impedisce di fare un raffronto fra vari amplificatori.

Per permettere il raffronto possiamo calcolare l'amplificazione intrinseca a vuoto che dipende unicamente da elementi interni all'amplificatore. Il calcolo dell'amplificazione intrinseca a vuoto è indicato in fig.17b.

Nella fig.17c e nella fig.17d sono riportati i calcoli della resistenza di ingresso e della resistenza di uscita dell'amplificatore in configurazione ad emettitore comune.

Per fare l'analisi dinamica utilizziamo il modello semplificato di fig.8a. 

Rispetto al caso precedente cambia il fatto che il condensatore di bypass  baypassa solo parte della resistenza di emettitore che pertanto è stata divisa in due parti, R_E1 ed R_E2  (fig.18).

I 2 condensatori di accoppiamento  ed il condensatore di bypass dello schema di fig. 18 costituiscono dei circuiti aperti per la corrente continua e dei corto circuiti per la corrente alternata alla frequenza del segnale che vogliamo amplificare.

Operiamo a centro banda, cioè in quell'intervallo di frequenze in cui l'amplificazione non dipende dalla frequenza. Nel circuito non ci sono cioè elementi reattivi; il circuito è solo resistivo. Inoltre i generatori di corrente continua e di tensione continua costituiscono anch'essi dei corto circuiti per il segnale. Sotto queste ipotesi possiamo , nel caso di fig.18 , eliminare i condensatori e considerare il generatore di tensione continua , massa per il segnale.

Per lo schema indicato a destra in alto nella fig.18 possiamo utilizzare il modello di sinistra in alto tratto dalla fig.8a. Il calcolo dell'amplificazione di corrente e di tensione è indicato in fig.18,  I valori ottenuti dipendono anche dal carico (altoparlante), da elementi cioè esterni all'amplificatore e ciò ci impedisce di fare un raffronto fra vari amplificatori.

Per permettere il raffronto possiamo calcolare l'amplificazione intrinseca a vuoto che dipende unicamente da elementi interni all'amplificatore. Il calcolo dell'amplificazione intrinseca a vuoto è indicato in fig.19.

Nella fig.20 e nella fig. 21 sono riportati i calcoli della resistenza di ingresso e della resistenza di uscita dell'amplificatore in configurazione ad emettitore comune con R_E .

Nella configurazione a  collettore  comune, rappresentata in fig.19, il segnale viene immesso fra base e massa tramite il condensatore C₁ e viene prelevato fra emettitore e massa tramite il condensatore C₂.

Il collettore , comune alla base ed all'emettitore , ai fini del segnale, è come se fosse collegato a massa, infatti il generatore della CC ha una resistenza interna molto bassa.

Possiamo analizzare il circuito di fig.19a dal punto di vista statico e dal punto di vista dinamico.

PUNTO DI VISTA STATICO

Nell'analisi statica si considera il circuito alimentato dalla sola corrente continua; il segnale è assente.

Nel circuito i condensatore è come se costituissero dei circuiti aperti.

il circuito di fig19a diventa pertanto come quello di fig.19b e quindi di fig.19c.

Considerando la fig.19c. , possiamo scrivere:

V_B = V_cc(R₂/R₁+R₂); considerando che V_BE = 0,7V  possiamo inoltre scrivere:

V_E = V_B-0,7 = V_cc(R₂/R₁+R₂) - 0,7 .

La tensione sul collettore è uguale alla tensione di alimentazione

 

 

PUNTO DI VISTA DINAMICO

ANALISI DI PICCOLO 

 

Per fare l'analisi dinamica utilizziamo il modello semplificato di fig.8a. .

I 2 condensatori di accoppiamento  ed il condensatore di bypass dello schema di fig.23  costituiscono dei circuiti aperti per la corrente continua e dei corto circuiti per la corrente alternata alla frequenza del segnale che vogliamo amplificare.

Operiamo a centro banda, cioè in quell'intervallo di frequenze in cui l'amplificazione non dipende dalla frequenza. Nel circuito non ci sono cioè elementi reattivi; il circuito è solo resistivo. Inoltre i generatori di corrente continua e di tensione continua costituiscono anch'essi dei corto circuiti per il segnale. Sotto queste ipotesi possiamo , nel caso di fig.23 , eliminare i condensatori e considerare il generatore di tensione continua , massa per il segnale.

Per lo schema indicato a destra in alto nella fig.23 possiamo utilizzare il modello di sinistra in alto tratto dalla fig.8a. Il calcolo dell'amplificazione di corrente e di tensione è indicato in fig.23 I valori ottenuti dipendono anche dal carico (altoparlante), da elementi cioè esterni all'amplificatore e ciò ci impedisce di fare un raffronto fra vari amplificatori.

Per permettere il raffronto possiamo calcolare l'amplificazione intrinseca a vuoto che dipende unicamente da elementi interni all'amplificatore. Il calcolo dell'amplificazione intrinseca a vuoto è indicato in fig.24. Nella fig.25 e nella fig.26  sono riportati i calcoli della resistenza di ingresso e della resistenza di uscita dell'amplificatore in configurazione a collettore comune.