balun
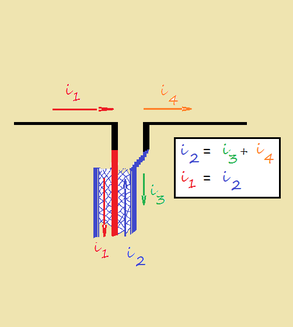
immaginiamo di avere una linea coassiale collegata ad un dipolo come in fig.1.
affinchè l'antenna possa avere un diagramma di irradiazione come dire, normale (vedi "Antenne") occorre che le correnti i1 e i4 che scorrono nei bracci del dipolo siano uguali.
Ora accade che nel cavo coassiale scorrono le correnti i1e i2 che sono uguali e contrarie, che i2 scorre nella superficie interna della calza ed interessa solo la parte superficiale di essa (effetto pelle), che i2, arrivato alla fine del cavo coassiale segue due strade, una è quella del braccio del dipolo (i4) a cui la calza è collegata e l'altra è la superficie esterna della calza (i3).
A questo punto il dipolo è percorso in un braccio dalla corrente i1 e nell'altro dalla corrente i4 diverse fra loro; il diagramma di irradiazione in queste condizioni assume una forma anomala; l'antenna irradia poco e male.
Vediamo come si può equilibrare la situazione, fare in modo cioè che i3 diventi pari a zero e che quindi i4 ed i1 siano uguali.
Per fare ciò occorre rendere molto alta l'impedenza della superficie esterna della calza del coassiale in modo che i3 si riduca drasticamente diventando in pratica nulla.. In altri termini occorre fare in modo che possa avvenire in modo corretto il collegamento fra il dipolo che è un elemento bilanciato, con il cavo coassiale che invece è sbilanciato.
per effettuare tale adattamento occorre utilizzare un qualcosa che renda ciò possibile questo qualcosa è il balun (balanced -unbalanced).
Il balun è quindi un dispositivo che sostanzialmente elimina la corrente i3 e rende uguali le correnti che sorrono nei due bracci del dipolo in modo che il diagramma di irradiazione si normalizzi.
esistono vari modi per realizzare un balun, in generale si può affermare che esistono due tipologie di balun, quelli costituiti da spezzoni di linea che solitamente funzionano in una specifica frequenza e quelli che invece utilizzano toroidi e bobine che estendono la gamma di frequenza di lavoro.
balun a trasformatore
In fig.2 è rappresentato un balun di tensione; trattasi in pratica di un trasformatore toroidale con rapporto 1:1 che assolve alla sua funzione primaria di eguagliare le correnti i1 ed i4 (fig.2).
dico funzione primaria perche può capitare di avere un trasformatore toroidale con rapporto diverso da 1:1 in tal caso esso assolve anche alla funzione di adattare l'impedenza del coassiale con quella dell'antenna.
Se per esempio l'impedenza dell'antenna è pari a 450Ω e quella del coassiale è pari a 50 allora un balun con rapporto 9:1 assolve oltre che alla sua funzione primaria a nche a quella di adattatore di impedenza.
Che questo tipo di balun annulli la i3 è evidente; le due correnti uscenti dal secondario del balun non possono che essere uguali ciò implica che i3 sia pari a zero.
Per calcolare il balun si opera in questo modo:
- si va sul sito "Toroids info" per la scelta del toroide in funzione della larghezza di banda che si vuole avere;
- si calcola il valore delle induttanze in μH, in funzione dell'impedenza dell'antenna e della linea , utilizzando la formula: L=Z/2πf;
- trovati i valori di L si applica la formula: L=(AL x turns2)/1000 riportata nel sito, dove AL è un coefficiente, sempre indicato nel sito, relativo al toroide .
- dalla formula indicata nel punto 3) si ricava il numero delle spire (turns) : turns=radq(Lx1000/AL) del primario e del secondario.
E' evidente che se l'impedenza della linea è uguale a quella dell'antenna, i due numeri delle spire (turns) trovati saranno uguali. Se invece le impedenze sono diverse otterremo due valori di turns, uno relativo al primario ed uno al secondario; in questo caso il balun funge anche da adattatore di impedenza.

Il trasformatore toroidale di fig.2 può essere montato come in fig.3 , il balun di tensione si trasforma allora in balun di corrente; c'è da notare che in questa configurazione non ci troviamo più in presenza di un trasformatore; il numero delle spire dei due avvolgimenti non può che essere uguale; il dispositivo non può in questo caso assolvere alla funzione di adattatore di impedenza ma la sua funzione si limita a quella di balun 1:1.
Cioè a quella di annullare la i3 .
calcolo della potenza con balun in ferrite
Parte dell'energia in transito si trasforma in calore e questo se è eccessivo può procurare la rottura del nucleo del balun.
Per tenere sotto controllo questo aspetto bisogna fare alcune considerazioni legate al flusso magnetico che dipende dalla sezione del nucleo, dal numero delle spire e dalla tensione applicata.
Esistono valori limite del flusso che vanno rispettati ; essi , per le ferriti sono indicati in tabella (fig. 3a).

la densità di flusso (induzione magnetica) si calcola utilizzando la seguente formula:
B max = (E x 102)/(4,44 x An x N x f)
Dove E è la tensione applicata , An è la sezione del nucleo in cm2, N il numero delle spire , f la frequenza in MHz.
balun con linea a λ/2

E' un balun semplice da realizzare è costituito da uno spezzone di linea lungo λ/2 collegato come in fig.4.
Lo scopo di questo spezzone è quello di far arrivare ai capi del secondo braccio del dipolo una tensione doppia rispetto a quella che si avrebbe senza balun.
Ciò è reso possibile dal fatto che nel percorrere lo spezzone lungo λ/2 la tensione accumula uno sfasamento di 180°, λ/2 appunto, e si presenta quindi al secondo morsetto di carico in opposizione di fase dandogli una tensione pari a 2V; non esiste alcuna corrente i3.
La potenza senza balun è : V2/Zo la potenza con balun è (2V)2/ZL , poichè le due potenze sono uguali, si deduce che
4Zo=ZL.; ciò he significa che questo balun è anche un adattatore di impedenza 4 : 1.
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta


