ANTENNE

Le antenne assolvono alla funzione di irradiare nello spazio circostante l'onda elettromagnetica "prodotta" dal trasmettitore (A.T. -antenna trasmittente-) e/o di captare l'onda elettromagnetica e portarla al ricevitore (A.R. -antenna ricevente-).
I due tipi di antenna funzionano nello stesso modo (fig.1), cioè hanno lo stesso guadagno, lo stessi diagramma di radiazione.. eccetera.
Questa, in buona sostanza, è al conclusione a cui si arriva col teorema di reciprocità l di Lorentz.

Un'antenna si comporta come un circuito risonante, ed avrà quindi un suo diagramma di risonanza (fig.1a), riuscirà a captare l'onda che avrà la frequenza pari a quella di risonanza o compresa nella banda passante., tutte le altre onde di frequenza diversa non potranno essere utilizzate.
Un'antenna può essere resa risonante in funzione della sua lunghezza; solo quando la sua lunghezza è pari ad un multiplo di λ/2.
Se il multiplo è 1 siamo in presenza di un dipolo a mezz'onda, quando è 2 o maggiore di 2 siamo difronte ad una long wire.

Quando un onda elettromagnetica che ha una frequenza pari a quella di risonanza dell'antenna, raggiunge l'antenna su di essa si formerà un' onda stazionaria di corrente che avrà le forme di fig. 1b.
Trattasi di onde stazionarie di corrente; la corrente scorrerà nel senso delle frecce rosse.
Questo è quanto avviene nelle antenne riceventi,
Se siamo, invece, in presenza di un'antenna trasmittente il segnale presente nella linea, se questa ha un'impedenza caratteristica pari all'impedenza di radiazione dell'antenna viene trasmesso integralmente nell'antenna nella quale, essendo essa configurabile come una linea aperta, si instaura un'onda stazionaria (fig.1b) che poi viene irradiata nello spazio circostante come onda elettromagnetica..
Insomma ricapitolando c'è un qualcosa che crea un campo elettromagnetico che viene irradiato dall'antenna trasmittente e captato da un'antenna ricevente..
Il campo elettromagnetico è quello della equazione di Maxwell.
l'antenna trasmittente irradia nello spazio in tutte le direzioni. l'onda elettro magnetica che si propaga in modo sferico; nella superficie di una generica sfera ( le sfere sono infinite) saranno presenti contemporaneamente il campo elettrico ed il campo magnetico rappresentati il primo da vettori (azzurri in in fig. 1bb) tangenti alle linee di forza del campo elettrico ed il secondo da vettori (rossi in fig.1bb) tangenti alle linee di forza del campo magnetico . I vettori rossi e azzurri sono perpendicolari fra loro. Il loro prodotto vettoriale genera il vettore di pointing che risulta perpendicolare al piano formato dai vettori rossi e azzurri e quindi , considerando la sfera di irradiazione, ha una direzione radiale
Questo vettore di pointing , come sapiamo, ha le dimensioni di una potenza su una superficie e si misura in W/m2. ricordiamo infatti che
- l'intensità del campo elettrico è pari a F/q che corrisponde alla forza necessaria a spostare una carica q immersa nel campo elettrico e che si misura in N/C (Newton/coulomb) = N m /C m = Volt / m .
- l'intensità del campo magnetico si misura in A/m.
Man mano che ci si allontana dall'antenna trasmittente le sfere diventano sempre più grandi la potenza irradiata di distribuisce su una superficie sempre più grande e l'intensità del campo diminuisce (attenuazione) non cambia invece la forma dell' onda irradiata.
l'attenuazione è direttamente proporzionale alla distanza, la potenza irradiata invece diminuisce col quadrato della distanza.
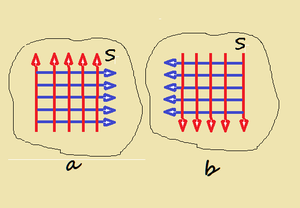
Dunque lontano dall'antenna trasmittente su una porzione S ( in fig.1bb è rappresentata la medesima porzione di superficie sferica S in due diversi momenti distanti fra loro di mezzo periodo) della superficie di una sfera troverò un'antenna ricevente che potrà essere influenzata dall'onda elettromagnetica che giace nella stessa porzione di superficie sferica che posso rappresentare coi suoi vettori di fig.1bb. che induce appunto una corrente nell'antenna.
Poiché l'onda elettrica e l'onda magnetica sono sinusoidali i vettori cambieranno periodicamente verso come si nota in fig 1bb a) e b). Si passa dalla situazione a) alla b) in mezzo ciclo.
Il vettore di Pointing è perpendicolare al piano del disegno ed è rivolto verso chi guarda.
L'intensità del campo Elettrico può essere espresso anche in decibel con riferimento ad un campo di 1μV/m.
Per esempio un 'intensità di campo di 500μV/m corrisponde a 20log(500/1) ≈ 54 db.
Utilizzando tale modo di misurazione dell'intensità del campo è agevole calcolare la tensione ai terminali di un ricevitore in termini di campo ricevuto .

Si utilizza la seguente espressione:
V (db) = S + X + Y -Z dove:
- V (db) è la tensione espressa in decibel del terminale del ricevitore;
- S è l'intensità del campo in decibel;
- X il rapporto , in decibel, derivante dal diagramma di fig 1bc .
- Y il guadagno in decibel dell'antenna relativo ad un dipolo a mezza lunghezza d'onda;
- Z in decibel le perdite della linea .
Se per esempio abbiamo a 20 MHz un campo di intensità S di 150 μV/m. corrispondente a 43,5 db , un'antenna con guadagno Y di 5db sul dipolo a mezz'onda, una linea con perdita Z di 2 db , possiamo calcolare V(db) dopo aver determinato dal diagramma di fig. 1bc in corrispondenza della frequenza 20 MHz il rapporto X fra l'intensità del campo e la tensione ai terminali del ricevitore che risulta pari a 7,6 db.
Risulta: V (db) = S + X + Y -Z = 43,5 + 7,6 + 5 - 2 = 54,1 db
54,1 db corrispondono a ~ 507 μV
alcune caratteristiche delle antenne
- Potenza irradiata: La potenza irradiata si ottiene integrando il vettore di Pointing S=HxE (W/m2.) su una superficie chiusa contenente l'antenna (vedi fig.1bb)
- Guadagno: parlando di guadagno sembrerebbe che l'antenna sia un amplificatore, in realtà l'antenna non amplifica ma prende l'energia disponibile della sorgente e la focalizza su un'area più ampia o più ristretta. Il guadagno di un'antenna viene definito come il rapporto fra la potenza irradiata nella direzione in esame e la potenza che irradierebbe un'antenna di riferimento nella stessa direzione se alimentata con la stessa potenza. Il guadagno può esprimersi in due modi:
- usando a riferimento un'antenna isotropa cioè che irradi in modo uguale in tutte le direzioni;
- utilizzando come antenna di riferimento un dipolo λ/2..
Nel primo caso si ha un guadagno assoluto e per la misura si utilizza il dBi; nel secondo si ha un guadagno relativo e si utilizza il dBd.
La relazione che lega il dBi al dBd è la seguente: dBi= dBd + 2,15. ciò significa che il dipolo di riferimento (punto 2) ha un guadagno rispetto all'isotropo (punto 1) di 2,15 dB.
Possiamo dire che le antenne in genere irradiano in certe direzioni più che in altre, quindi rispetto alla antenna di riferimento hanno guadagno variabile con la direzioni; il guadagno è quindi funzione della direzione di osservazione. In pratica però si considera il guadagno nella direzione di massima irradiazione; il guadagno (massimo) così inteso se moltiplicato per la potenza trasmessa da luogo ad un parametro noto come EIRP (Equivalent Isotropic radieted power) che è una densità di potenza radio.
Il guadagno essendo il rapporto fra due grandezze omogenee ha le dimensioni di un numero, il suo valore può esprimersi in dB,
Per esempio un guadagno di 2 corrisponde a 3 dB. infatti 10log(2)=3dB
- Direttività: la direttività di un'antenna in una certa direzione è il rapporto fra l'intensità di radiazione in quella direzione e la potenza totale irradiata (in tutte le direzioini).
- Resistenza di radiazione: l'antenna irradia potenza Pr nello spazio, se immaginiamo di far assorbire tutta la potenza irradiata da una resistenza Rr otteniamo la resistenza di radiazione. tale resistenza è pari evidentemente a Rr = V2/Pr = Pr/I2.
- Resistenza di dissipazione: non tutta la potenza dell'antenna viene irradiata nello spazio, parte di essa, Pd, viene dissipata; la resistenza di dissipazione è pari a Rd = V2/Pd = Pd/I2.
- Impedenza caratteristica: L'impedenza caratteristica ha la seguente espressione: ZL = (Rr+Rd) + j XL il primo termine, che costituisce la parte reale dell'espressione, è la resistenza ohmica; il secondo termine (parte immaginaria) è la reattanza dell'antenna. Ogni tipo di antenna ha la sua impedenza caratteristica che è necessario conoscere al fine di adattarla a quella della linea di trasmissione; bisogna fare ciò affinché l'onda non venga riflessa indietro verso il trasmettitore con possibili danni allo stesso; con le radio riceventi il mancato adattamento non pone il problema del danneggiamento ma quello relativo ad una cattiva ricezione.
- Coefficiente di riflessione: il coefficiente di riflessione indica quanto l'onda viene riflessa; esso è pari a : Γ= (ZL-Z0)/(ZL+Z0) dove ZL è l'impedenza dell'antenna e Z0 l'impedenza caratteristica della linea. Il suo valore varia fra -1 quando ZL è uguale a 0 e 1 quando ZL è uguale a ∞. Quando Γ = 0 l'antenna è perfettamente adattata alla linea..
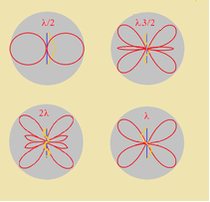
- Diagramma di radiazione: il diagramma di radiazione è la rappresentazione tridimensionale del guadagno.

Area efficace:
L'area efficace, chiamata anche sezione trasversale di assorbimento, è un parametro molto utile in ricezione e rappresenta il rapporto fra la potenza estratta e la densità del flusso incidente (vettore di Pointing), cioè Aeff= Pr /Si . l'area efficace è una percentuale dell'area geometrica ed è legata al guadagno dall'espressone Aeff= Gr λ2/4π. da quest'ultima relazione ricaviamo il guadagno Gr dell'antenna ricevente : Gr = Aeff 4π/λ2 ; il guadagno dell'antenna trasmittente è pari a: Gt= Si/(Pt /4πR2) ; dall'espressione di Aeff ricaviamo Pr =Aeff Si . poichè Si = Pt Gt/4πR2 ; possiamo scrivere Pr =Aeff Pt Gt/4πR2 ; introducendo in quest'ultima formula Aeff= Gr λ2/4π otteniamo : Pr = GrPt Gt(λ/4πR)2
Antenne a filo
Possiamo individuare due tipologie di antenne, quelle elettriche che ricavano la loro energia dal campo elettrico dell'onda elettromagnetica. e quelle magnetiche che la ricavano invece dal campo magnetico dello stesso.
Le antenne a filo ricavano la loro energia dal campo elettrico e pertanto sono antenne elettriche..
A conferma di quanto detto possiamo ricordare le leggi sul magnetismo affermano in sostanza che i conduttori messi in un campo elettrico variabile divengono sede di una f.e.m. che provoca il passaggio di una corrente; (questo è il principio di funzionamento delle antenne a filo) ed inoltre che una spira o una bobina immersa in un campo magnetico variabile diviene sede di una corrente, per via della variazione del flusso magnetico, che è proporzionale ad esso.
DIPOLO A λ/2 (Hertziano)

E' un'antenna costituita da due bracci alimentata al centro (fig.2).
Il dipolo si comporta come una linea di lunghezza λ/2 coi morsetti d'uscita aperti; per questo motivo si instaura un'onda stazionaria che, per via della lunghezza λ/2 ha un massimo di corrente nel punto centrale (ventre di corrente); la corrente si annulla poi agli estremi (nodi di corrente).
La tensione ha un comportamento contrario, ha un minimo al centro (nodo di tensione) e due massimi agli estremi (ventri di tensione) .
L'impedenza di ingresso dell'antenna è funzione della lunghezza complessiva (l+l) dei bracci, del rapporto fra tale lunghezza ed il diametro del conduttore con cui è realizzata l'antenna e della distanza s fra i bracci.
L'impedenza d'ingresso è data dalla formula:
Zi= 73,2 + j42,5 Ω.
73,2 è la resistenza di irradiazione del dipolo a mezz'onda j42,5 è la parte immaginaria dell'impedenza.
La presenza di una reattanza significa che l'antenna a mezz'onda non è perfettamente risonante; per renderla risonante (eliminare la parte reattiva) bisogna accorciarla ( j42,5 è positivo ; è quindi una induttanza) e portare la lunghezza complessiva a circa K x λ/2. ; la costante K che è K<1 vale circa 0,93 per il rame e circa 0,83 per l'alluminio; accorciandola a tale valore la parte reale dell'impedenza, cioè la resistenza di irradiazione, diventa:
Ri= 73,2 - (10.000 / 120 ln (4 x l /d)), con d diametro del filo del dipolo ed l = K x λ/2. .
(trattasi di una formula empirica).
Quindi se devo ricevere un'onda a 14MHz con λ= 21,428 mt per avere un dipolo perfettamente risonante devo dargli una lunghezza di 0,93 x 21,428/2 = 9,96 mt.
In questo modo la parte reale della sua impedenza sarà:
Ri = 73,2- (10.000/120ln(4l/d)) Ω e la parte immaginaria sarà pari a zero.

Quanto detto è valido se il dipolo è installato in spazio libero; se invece è posizionato vicino al terreno , occorre tener conto del grafico di fig. 3.
Immaginiamo un dipolo con diametro del cavo di 3 mm, a 10 mt dal suolo λ = 40 mt, applicando le formule viste abbiamo:
lunghezza del dipolo:
l + l = 0,93 x λ/2 = 18,6 mt;
dal grafico di fig.3 ricavo, per un'altezza di 10mt (0,25λ), una resistenza pari a 80Ω; allora la Resistenza di irradiazione Ri = 80 - (10.000 / 120 x ln (4l/d)) = 71,15 Ω.
poichè la linea di alimentazione ,(cavo coassiale), ha un'impedenza di 50 o 75 Ω , le cose vanno abbastanza bene.; si trattera poi, tenuto conto che la linea è sbilanciata e l'antenna bilanciata, di montare un balun 1:1.
Il dipolo come tutte le antenne ha una frequenza di risonanza; se la frequenza di lavoro è inferiore a quella di risonanza il circuito è capacitivo se invece è maggiore il circuito risulta induttivo. possiamo quindi individuare la larghezza di banda di un'antenna che rappresenta la sua attitudine a funzionare entro una gamma più o meno vasta di frequenze.

C'è da osservare che l'antenna funziona anche con le armoniche di ordine dispari; come si vede infatti in fig.4 al centro del dipolo con queste armoniche ho un ventre di corrente e quindi l'impedenza minima che attiene a quel dipolo (intorno ai 70Ω) ; esattamente come avviene con la fondamentale che tra l'altro è la prima armonica e quindi dispari.
L'impedenza agli estremi del dipolo è molto alta e si aggira intorno ai 5.000, 6.000 Ω.
Con le armoniche pari invece al centro del dipolo ho un nodo di corrente cui corrisponde una resistenza di 5.000, 6.000Ω; non potrei collegarla quindi ad un cavo coassiale che ha un'impedenza compresa fra i 50 ed i 75 Ω a meno di adattare l'impedenza dell'antenna a quella del cavo coassiale.

Prendiamo in considerazione un dipolo a mezz'onda progettato per i 40 mt (7,5 MHz) (fig.4a), alimentandolo al centro (ventre di corrente) potrei utilizzarlo per due sole frequenze; 7,5 Mhz (prima armonica) e (7,5 x 3) MHz (terza armonica ) .
Se invece di alimentare il dipolo al centro lo alimentassi all'estremità (ventre di tensione) potrei captare tutte le armoniche, pari e dispari ; avrei solo il problema di adattare l'altissima impedenza dell'antenna all'impedenza del cavo coassiale; e questo è possibile.
DIPOLO CORTO

Trattandosi di un dipolo corto certamente non è risonante e pertanto l'espressione della la sua impedenza assume la seguente forma :
Zi= R+jX dove R è la resistenza di radiazione e X la parte immaginaria dell'impedenza.
Questa parte immaginaria è certamente una reattanza capacitiva essendo il dipolo corto.
Abbiamo visto che la resistenza di radiazione Ri di un dipolo a mezz'onda è pari a 73,2Ω se il dipolo è in spazio libero cioè se la sua distanza dal suolo è maggiore di 2λ; se invece la distanza dal suolo è minore di 2λ la resistenza di radiazione Ri si ricava dal grafico di fig.3.
Se ora consideriamo un dipolo corto in cui L < λ/2 (fig.5) per ottenere la resistenza Ri occorre moltiplicare 73,2Ω (se il dipolo è in spazio libero) oppure il valore inΩ ricavato dal grafico di fig.3 (se il dipolo è ad una distanza dal suolo inferiore di 2λ), per il coefficiente K ottenuto dal grafico di fig. 7

Supponiamo per esempio di avere un dipolo con l= 5 mt , a 4,5 mt di distanza h dal suolo e di volerlo far operare a 40 mt (7,5 MHz , λ= 40 mt).
Dal grafico di fig. 3 per 4,5/λ =0,11 ottengo Ri=28Ω;
Dal grafico di fig.6 per 10/40 = 0,25 ottengo K = 0,18
Utilizzando questi valori ottengo una resistenza di radiazione effettiva di:
Ri(eff)= 28 x 0,18 = 5,04.
Poichè il dipolo è corto l'espressione della impedenza di ingresso sarà un numero complesso del tipo:
Zi= Ri(eff) + j Xi.
Come si calcola Xi?
Per calcolare Xi si usa la formula:
Xi = -JZocotg(βL/2) con β = 2π/λ , dove:
Zo = 276log (2l/(d x radq(1+(2l/4h)2))).
dove l è la lunghezza di un braccio del dipolo d il diametro del filo usato h l'altezza sul suolo.
Quindi risulta:
Zo= 1.112Ω ; Xi= 1.112Ω; l'espressione dell'impedenza d'ingresso è:
Zi= 5,04 - j1.112 Ω
ora abbiamo una reattanza capacitiva che va eliminata con l'aggiunta di una reattanza induttiva dello stesso valore; rimane la resistenza che va adattata a quella della linea.
Vediamo di calcolare l'induttanza da aggiungere:
sappiamo che ZL = 2πfL ; L= 1.112 / 2 x π x 7.500.000 = 23μH.
L'induttanza va inserita nel circuito come in fig.5.
E' bene inserire un balun che faccia anche da adattatore di impedenza.
ANTENNA WINDOM

Questa antenna venne progettata e realizzata da Loren G.Windom , un radioamatore statunitense..
Windom verificò che, portando il punto di alimentazione al 36% della lunghezza del dipolo, in quel punto la corrente aveva un valore ancora elevato e che la resistenza assumeva un valore abbastanza basso di circa 300Ω.
Quel punto venne chiamato "presa calcolata" ed ha la caratteristica che in esso le armoniche pari sebbene non abbiano un ventre hanno un valore abbastanza elevato che si avvicina molto a quello del ventre di corrente.
Ora se viene ricevuta la frequenza di 3,6 MHz (80 mt) quella cioè per cui è stato calcolato il dipolo (L=λ/2 = 40mt), vengono ricevute anche le frequenze pari 3,6x2 =7,2, 3,6x4=14,4, 3,6x6=21,6 e 3,6x8=28,8 MHz; queste frequenze sono quelle utilizzate dai radio amatori (vedi fig.8) non vengono invece ricevute le armoniche dispari diversamente da quanto avviene nel dipolo a mezz'onda alimentato al centro.
E' evidente che la resistenza di 300 Ω va adattata a quella del cavo coassiale di alimentazione di 50 Ω.
Per far ciò si può utilizzare un balum di tensione 6:1 (300/50 = 6) che oltre che rendere sbilanciata l'antenna funge anche da adattatore di impedenza.
Insomma Windom ha progettato un'antenna multi banda per radioamatori.
DIPOLO A λ/4 (Marconiano)

E' in buona sostanza un dipolo verticale a mezz'onda con il braccio verso terra sostituito dalla riflessione che di esso ne fa il terreno supposto ottimo conduttore (fig.9).
La sua lunghezza diventa allora pari a λ/4.
L'espressione della resistenza di irradiazione vale:
Ri = 36.6 + j 21,25 .
ed uguale a Ri/2 del dipolo a mezz'onda..
Valgono tutti i ragionamenti fatti per il dipolo a mezz'onda e cioè:
- per rendere perfettamente risonante quest'antenna bisogna accorciarla moltiplicando λ/4 per la costante K;
- che accorciandola la parte reale di Ri diminuisce ed arriva ad un valore di 34 ÷35Ω .
DIPOLO TRAPPOLATO

E' un dipolo multibanda.
Immaginiamo di voler ricevere 7 e 14 MHz, utilizzo il dipolo c-c di fig.9a per ricevere i 14 MHz ed il dipolo a-a per ricevere i 7 MHz; c-c e a-a sono due dipoli a mezz'onda.
Ciò è reso possibile dal fatto che vengono poste sul dipolo due trappole ( circuiti risonanti paralleli) in posizione come in fig.9a aventi frequenza di risonanza pari a 14 MHz..
Quando sintonizzo i 14 MHz la trappola blocca la frequenza di14 MHz e fa funzionare solo il dipolo a-a. (i tratti b e come se non ci fossero).
Quando sintonizzo i 7 MHz le due trappole non danno alcun contributo, e come se con ci fossero e funziona pertanto il dipolo c-c.
Per calcolare la lunghezza dei bracci a e b si opera così:
a= (142,5 /14)/2 = 5,089 mt (142,5 = 300 x K /2);
c= (0,839 X 142,5 /7)/2 = 8,539 mt;
b= C-A = 3,450 mt

Per calcolare la trappola, costituita da un circuito LC risonante parallelo, si utilizza la nota formula :
f=1/2πradq(LC); fissando un valore alla capacità C si ottiena il valore di L.:
per C=20 pF si ha:
L= 1/4π2Cf2 = 6,46 μH
In fig.9b sono raffigurati due possibili modi di realizzare una trappola.
In alto la trappola è formata da una induttanza costituita da un filo in rame di opportuno diametro avvolto in un tubo in PVC ed il condensatore è costituito da una piastrina in vetronite ramata da entrambe le parti.
In basso la trappola è costituita da un cavo coassiale avvolto intorno ad un tubo in PVC e collegato come indicato; il cavo è dello stesso tipo del cavo della linea.
DIPOLO A λ INTERA

l'antenna ad onda intera rappresentata in fig.10 ha nel centro un nodo di corrente ed un ventre di tensione, in quel punto dunque ha una impedenza elevata aggirantesi su 6.000 Ω; è bene alimentare questa antenna ad una distanza λ/4 dall'origine dove si ha un ventre di corrente ed un nodo di tensione con un valore di impedenza simile a quello della linea a cavo coassiale di alimentazione (50÷70Ω)..
Antenne magnetiche
Abbiamo detto che una spira o una bobina immersa in un campo magnetico variabile diviene sede di una corrente che è proporzionale alla variazione del flusso.
Questo è il principio di funzionamento delle antenne magnetiche
S.T.L. Small Trasmitting Loop

Se il circuito a di fig.11 viene eccitato da un'onda elettromagnetico l'energia interessa il condensatore e l'induttanza; quando il condensatore è carico l'energia assume la forza di un campo elettrico, quando il condensatore si scarica sull'induttanza si ngenera una corrnte che forma un campo magnetico e l'energia allora assume la forma di un campo magnetico, la corrente continua poi a scorrere verso il condensatore ricaricandolo, questi, , una volta carico si scarica dinuovo attraverso l'induttanza e così via; l'energia in sostanza si trasforma alternativamente in campo elettrico ed in campo magnetico.
Questo processo genera un campo di induzione nelle immediate vicinanze del circuito che si attenua velocemente in funzione della distanza da esso. l'attenuazione è inversamente proporzionale al cubo della distanza.
Questo circuito non crea però un campo di irradiazione o meglio crea un campo di irradiazione ridottissimo che comunque si attenua in modo inversamente proporzionale al quadrato della distanza,

Se si ntrasforma il circuito a nel circuito b e poi, stiranmdolo ulteriormente , nel circuito c la capacità C e l'induttanza L si distribuiscono uniformemente lungo il filo.
Il circuito originario si trasforma in un'antenna.
Intorno all'antenna avremo sempre un campo di induzione che però si esaurisce rapidamente allontanandosi dall'antenna.
Come sappiamo in questa zona (campo vicino) il campo di induzione è molto più grande del campo di radiazione (che in pratica non esiste) è la zona in cui l'antenna immagazzina energia elettrica e magnetica che viene scambiata, sotto forma di potenza reattiva, col generatore che la alimenta.
Come sappiamo la presenza di un corpo estraneo in questa zona altera fortemente le caratteristiche dell'antenna a causa del forte accoppiamento che sottrae energia alla fonte., esistono cioè notevoli perdite capacitive dovute alla vicinannza della terra.
Ecco perchè l'antenna va allontanata dalla terra.
Ora se noi concentriamo la capacità in un condensatore e sistemiamo il circuito come in fig. 12 abbiamo una riduzione delle perdire capacitive a vantaggio dell'energia che può essere irradiata dal filo posto ad anello.
A questo punto se l'antenna di fig.12 viene posta verticalmente (polarizzazione verticale che diviene orizzontale per angoli elevati) e col condensatore verso l'alto, viene influenzata pochissimo dalla vicinanza della terra e può irradiare senza che a questa irradiazione venga sottratta eccessiva potenza.
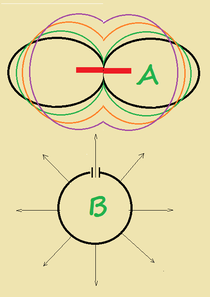
L'antenna di fig. 12, se posta su un piano verticale irradierà radialmente come in fig.12a,B. e potrà essere utilizzata per collegamenti a lunga ed a breve distanza; sotto angoli di irradiazione bassi presenta una direttività maggiore come si nota in fig. 12a,A.
il diagramma nero è quello relativo ad un angolo di irradiazione pari a zero passando ai grafici verde , arancione , granata, nell'ordine, il grafico diventa sempre più ellitico e la direttività diminuisce.
Quando l'antenna viene posta su un piano orizzontale (polarizzazione orizzontale), il diagramma di radiazione diventa circolare. ma con un angolo ridotto.
La resistenza di radiazione di un'antenna di questo tipo è molto bassa e si ricava dalla formula:
Rr = 391,6 x 10-8 x (F2 x A )2
dove Rr è la resistenza di radiazione in Ω , A è l'area circostritta dalla spira in m2, F la frequenza in MHz .
La resistenza di radiazione risulta molto piccola un centinaio di volte minore di quella delle antenne "elettriche".
L'antenna irradia dunque sotto una resistenza molto bassa l'energia che riceve dal trasmettitore; le correnti in gioco per questo motivo sono molto elevate ed è quindi necessario che il conduttore abbia un diametro elevato (effetto pelle) per evitare notevoli perdite in calore.,
La resistenza di perdita è data dalla formula:
Rp = 90,91 x 10-4 (F x G/d)
dove Rp è la resistenza di perdita in Ω, F la frequenza in MHz , G la lunghezza del conduttore in m, d il diametro del conduttore in m.
Il fattore di merito di questa antenna è molto elevato; l'antenna ha quindi un larghezza di banda molto limitata.
Per questo motivo è necessario rendere molto agevole la manovra del condensatore variabile.
Il massimo di eficienza con questa antenna lo si raggiunge con una lunghezza della spira pari a λ/4.
Questa antenna ha un guadagno rispetto al radiatore isotropico di 1,75 dbi; che non è molto diverso dal guadagno di un dipolo a mezz'onda che è pari a 2,15 dbi.
ANTENNA A QUADRO

L'antenna a quadro è un'antenna magnetica; è costituita da una bobina piatta con dimensioni non trascurabili rispetto a λ.
Se è di dimensioni piccole ha poca attitudine ad irradiare o ad assorbire energia elettromagnetica.
Se colleghiamo i punti A e B di fig.11 ad un trasmettitore le correnti indicate in rosso risultano uguali e, se L è molto piccolo, sfasate di 180°.
In queste condizioni i campi magnetici creati dalle due correnti risultano uguali e contrati e pertanto si elidono a vicenda..
Se invece L è sufficientemente grande lo sfasamento non è più di 180° ma è pari a π-2πL/λ; però poichè il termine 2πL/λ è molto piccolo il campo magnetico prodotto sarà anch'esso m,olto piccolo.
Nonostante il campo prodotto risulti ridotto, poichè la resistenza elettrica è anch'essa molto bassa il rendimento delle oscillazioni che si instaurano è elevato e quindi la trasmissione è possibile, beninteso per piccole potenze nel campo delle onde medie e per onda diretta.
Questo per quanto attiene alla trasmissione, che comunque non è il campo di applicazione di queste antenne, per ciò che riguarda invece la ricezione possiamo affermare che le cose vanno molto meglio.
Quando l'antenna si trova immersa in un campo elettromagnetico l'ampiezza del segnale captato aumenta col numero delle spire , con l'aumento della superficie racchiusa fra dii esse e diminuise con l'aumento della lunghezza d'onda, in formula: V=2πnS/λ
Se fra i punti A e B di fig.13 poniamo un condensatore variabile è possibile ricevere l'intera gamma delle onde medie.
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta


