Grandezze caratteristiche dei circuiti elettrici
La resistenza
Gli elettroni muovendosi ordinatamemte all'interno di un conduttore formano la corrente elettrica di conduzione ; nel lor cammino gli elettroni trovano una certa resistenza R dipendente dalla natura del conduttore che si riscalda.
La legge di Ohm afferma che la resistenza è pari al rapporto costante fra il potenziale V e la corrente I cioè R=V/I .
La potenza dissipata P= RI2 , si trasforma in calore.
La resistenza inoltre, dipendendo dalla natura fisica del conduttore può esprimersi nel seguente modo: R=ρ x l/S dove ρ è la resistività del conduttore , S la sezione del conduttore ed l la lunghezza del conduttore .
Le espressioni su indicate valgono per la corrente continua; per la corrente alternata occorre introdurre il concetto di valore efficace; Il valore efficace della corrente alternata è il valore espresso in amper di quella corrente continua che percorrendo una resistenza dello stesso valore, nel medesimo tempo, dissipa la medesima energia.
Possiamo definire il valore efficace di una funzione continua x(t) la media quadratica sul periodo della stessa x(t).
La media quadratica corrisponde alla radice quadrata della media dei quadrati.
Sotto questa ipotesi possiamo scrivere R= P/Ieff2 e quindi R= Veff/Ieff .
Supponendo che l'espressione della corrente alternata sia i= Imax sen ωt possiamo scrivere che P=Pmax/2 e pertanto RIeff2=RImax2/2 da cui Ieff= Imax/ radq(2)
Solitamente la resistenza di un conduttore aumenta con la temperatura secondo la seguente formula :
Rθ 2=Rθ 1(1+α Δ θ) dove α è un coefficiente di solito positivo per i
conduttori (αrame = 0,0042 ; αargento= 0,0036) e negativo per il germanio
ed il silicio.
Nella tabella sottostante sono riportati i valori della resistività di alcuni conduttori.

Legge di Ohm

Vediamo di arrivare alle leggi di Ohm partendo dalla velocità di deriva.
Sappiamo che la velocità di deriva è proporzionale al campo elettrico; è cioè:
Vd= -μE dove μ è la mobilità dell'elettrone, e che E=V/L
Guardando la fig.1 ci poniamo la domanda:
Quanti elettroni Δn passano nel tempo Δt attraverso la sez. A ?
Evidentemente passano tutti gli elettroni che si trovano nel cilindro:
avente il volume pari a : Vd Δt A
il numero di elettroni passanti sarà pari ad n che rappresenta il numero di elettroni per unità di volume , per il volume Vd Δt A.
Quindi sarà Δn = n Vd Δt A.
la carica è Δq = -q Δn = -q n Vd Δt A.
So che I = Δq/Δt = -q n Vd A. = q n A μ E;
poiché E = V/L posso scrivere: I = q n A μ V/L = (q n A μ / L) V
dove (q n A μ / L) =1/R è l'inverso di una resistenza cioè una conduttanza .
scrivo allora I R = V che è la prima legge di Ohm
Se prendo in considerazione l'espressione (q n A μ / L) =1/R posso scrivere:
R= L/q n A μ = (L/A) ( 1/ (q n μ ))
l'espressione 1/(q n μ) = ρ.
ρ è la resistività del materiale; la resistenza diventa allora :
R= ρL/A questa espressione è la seconda legge di Ohm.
Mobilità dell'elettrone
Sappiamo che la velocità di deriva è proporzionale al Campo Elettrico e che la costante di proporzionalità è μ, sappiamo cioè che Vd= -μE.
Ma quanto vale μ ?
Il valore di μ varia a seconda del metallo da 10 a 1000 cm2/Vs.
Non è un valore particolarmente alto e quando si dice che un metallo conduce bene ciò dipende dal fatto che è molto alto il numero di elettroni su centimetro cubo.
Questo numero è pari a circa 1022 elettroni/cm3 , esso dipende dal numero di Avogadro pari a 1023 elettroni/mole, la mole equivale infatti a circa un cm3.
Valore efficace di una funzione sinusoidale
Si definisce valore efficace ( Veff ) di una funzione continua x(t), la media quadratica (ovvero la "radice della media dei quadrati", in inglese root mean square, da cui la sigla RMS, da non confondere con il valor(e) quadratico medio, in inglese mean square, che è semplicemente la media dei quadrati), sul periodo della funzione stessa ; in una funzione sinusoidale è pari a Vmax / √2

valore efficace di una funzione triangolare

effetto pelle
La resistenza di un conduttore a sezione circolare di diametro D percorso da corrente alternata di frequenza f è pari alla resistenza di un conduttore cavo avente sezione circolare di diametro esterno D e spessore δ.
La resistenza di un tale conduttore cavo di lunghezza L è pari a :
R = ρ.L/S dove S , area della corona circolare di diametro esterno D e di diametro interno D-2δ, è pari a
δ.π.(D-δ), circa uguale a δ.π.D.
Per calcolare δ si usa la formula δ =√(2 ρ/ω.μ).
mettendo nell'espressione di R i valori indicati, otteniamo:
R = (L/π.D).√(ω.μ.ρ/2)
In questa formula μ è la permeabilità magnetica assoluta del conduttore che per i comuni conduttori è pari a quella nel vuoto (4.π.10-7 H/m) , ρ la sua resistività e D il diametro e δ la profondità oltre la quale non scorre la corrente; la corrente scorre solo in superficie da cui il termine "effetto pelle".
Il fatto che la resistenza del conduttore aumenti con la frequenza lo si può spegare supponendo di suddividere il conduttore in tanti tubicini aventi ciascuno sezione uguale e ridottissima; se i tubicini supposti separati ed uniti solo all'estremità vengono percorsi da una corrente continua ciascuno sarà percorso dalla medesima corrente avendo tutti la medesima resistenza; se invece il conduttore viene percorso da una corrente alternata i tubicini interni, essendo concatenati con un flusso maggiore, avranno maggiore impedenza e verranno percorsi da minore corrente rispetto a quelli esterni ; insomma la corrente con l'aumentare della frequenza tenderà a scorrere sempre più sulla superficie esterna del conduttore.
Un metodo per ridurre l'effetto pelle è quello di utilizzare il filo Litz.
Il filo Litz è un trefolo di conduttori singolarmente isolati (rame smaltato) aventi diametro minore della profondità dell'effetto pelle in modo tale che tale effetto venga ridotto al massimo.
Il modello di tessitura e torsione dei fili conduttori costituenti il trefolo è tale da ridurre gli effetti del campo magnetico generato dalla corrente alternata di elevata frequenza.
L'induttanza
Il flusso Φ è proporzionale alla corrente che lo produce cioè Φ = L1.I dove L1 rappresenta l'induttanza di una spira; ricordando che la legge fondamentale della induzione elettromagnetica è :
e = -N.dΦ/dt , possiamo scrivere:
dΦ/dt = - Ldi/dt e quindi e = - Ldi/dt con L= N.L1 .
Per quanto sopra si può scrivere che L1=Φ/I e che L=N.Φ/I ed N il numero
delle spire.
Ricordando che : Φ=B.S ; B=μH ; H=N.I/l possiamo scrivere :
μ=B/H=Φ.l/N.I.S = L.l/N2.S ; da questa espressione ricaviamo il valore di L=μ.N2.S/l.
Ricordando ora che μ=μ0.μr e che Ril =μr.l/S possiamo scrivere : L=μ0.N2/Ril=μoμr.N2.S/l
Una bobina ideale corrisponde ad una induttanza perfetta nella quale la corrente è sfasata in anticipo di π/2 rispetto alla tensione.
In realtà però un' induttanza perfetta non esiste.

In una induttanza reale infatti esistono varie cause di perdita di energia che risiedono principalmente nel materiale magnetico sottoposto al campo magnetico, se utilizzato per aumentare l'induttanza, (La Rrm è una resistenza che perrcorsa da una medesima corrente istantanea i della induttanza , assorbe in ogni istante una energia uguale a quella in realtà assorbita dal materiale magnetico), nella resistenza homica del conduttore Rrs da considerare in serie con essa e nella resistenza di isolamento delle varie spire affiancate Rrp da considerare invece in parallelo come indicato in fig.1.

C'è da porre in evidenza che la bobina reale di fig.1 può essere vista in uno dei due modi riportati in fig.2 cioè può essere rappresentata da un circuito equivalente costituito da una induttanza
ideale e da una resistenza in serie oppure da una induttanza ideale e da una resistenza in parallelo.
Prendiamo in esame i circuiti equivalenti serie e parallelo e per essi tracciamo i diagrammi di fig.3.
In tali diagrammi è stata determinata la tensione V per il circuito equivalente serie e la corrente I per il circuito equivalente parallelo.

Dall'analisi dei grafici si possono determinare i seguenti valori:
δ= tgδ=Rs/ωL=ωL/Rp; tgφ=ωL/Rs=Rp/ωL,
dove δ, molto piccolo e quindi confondibile con la sua tangente, è l'angolo di perdita e φ è lo sfasamento fra
corrente e tensione.
Per definire l'efficienza di una bobina si usa l'espressione:
Q=ωL/Rs = Rp/ωL = tgφ
chiamato "coefficiente di qualità" o "fattore di merito" o "coefficiente di sovratensione" di una
bobina.
C'è da osservare che, a causa delle perdite che producono, l'utilizzo dei materiali magnetici è da evitare per le frequenze elevate ; d'altro canto per le alte frequenze sono richiesti valori di induttanza ridotti per cui l'impiego di materiale magnetico non è richiesto.
L'energia di un induttore è pari a 1/2(LI2); corrisponde al lavoro necessario per far scorrere in esso una corrente I.
L'espressione dell'energia si ottiene in questo modo:
dv = Ldi/dt; dv dt =Ldi , moltiplicando per i si ha:
idv dt = Li di ; integrando abbiamo ∫Li di = 1/2(LI2).
La mutua induzione fra due circuiti
Supponiamo che i circuiti (bobine) 1 e 2 siano percorsi dalle correnti I1 e I2 e che si influenzino reciprocamente;
Sia e1 la f.e.m. indotta nel circuito 1 dal flusso generato dal circuito
2 che si concatena col circuito 1 ; possiamo scrivere :
e1= N1e'1=N1dΦ/dt
Il flusso Φ generato dal circuito 2, ricordando le seguenti formule :
Φ=B.S ; B=μ.H=μo.μr.H ; H=N2.I2/l ,
ha la seguente espressione :
Φ= μo.N2.I2/Ril.
Sostituendo l'espressione di Φ nella formula di e1 otteniamo:
e1=(μo.N1.N2/Ril).di2/dt =MdI2/dt ;
dove M=μo.N1.N2/Ril .
Con analogo ragionamento , considerando la f.e.m. indotta nel circuito 2 dal flusso generato dal circuito 1 che si concatena col circuito
2 possiamo ricavare l'espressione:
e2=(μo.N1.N2/Ril).di1/dt =MdI1/dt ;
dove M=μo.N1.N2/Ril .
Se l'intero flusso è concatenato con entrambe le bobine significa che l'intero circuito magnetico è il medesimo per entrambe e quindi anche la riluttanza Ril è la stessa; allora riprendendo le relazioni:
L1=μo.N12/Ril; L2=μo.N22/Ril; M=μo.N1.N2/Ril si
ricava:
M2=L1.L2; M=radq(L1.L2)
Quando il flusso comune è solo una parte del totale possiamo scindere l'induttanza di ciascuna bobina in due addendi; uno relativo al flusso comune ( L'1 ; L'2) ed uno dovuto al flusso creato
dalla propria corrente e che si concatena solo con la bobina che l'ha generato (L''1 ;
L''2) ; possiamo quindi scrivere che L1=L'1+L''1 e che L2=L'2+L''2 .
I termini L''1 ed L''2 sono le induttanze dovute al flusso disperso.
Poichè la mutua indizione è dovuta al flusso comune possiamo scrivere:
M=radq(L'1.L'2) < di radq(L1.L2).
Il rapporto k=M/radq(L1.L2) si chiama coefficiente di accoppiamento
fra le due bobine .
Bobine in serie
Supponiamo di avere due bobine L1 ed L2, nelle quali vi sia una mutua induzione, percorse dalle correnti I1e I2 ; le f.e.m. indotte nelle due bobine sono:
e1= L1.dI1/dt +- MdI2/dt ; e2=
L2.dI2/dt +-MdI1/dt
dove le f.e.m. di mutua induzione si sommano o si sottraggono a seconda che i flussi delle due bobine siano concordi o contrari.
Se le due bobine sono collegate in serie (VARIOMETRO) vengono percorse dalla medesima corrente e pertanto la
f.e.m. totale sarà:
e= e1+e2= (L1+L2+-2M)dI/dt
ed il coefficiente di autoinduzione totale sarà:
L=L1+L2+-2M.
Da questa espressione si deduce che in teoria l' induttanza totale L , se L1= L2=L0 e se il coefficiente di accoppiamento K è pari a 1 , varia fra il valore 0 ed il
valore 4L0 .
E facile trovare i valori minimo e massimo di L per valori di k minori di 1.
Campo elettrico
Prendiamo in esame due cariche elettriche q1 e q2 in due punti dello
spazio distanti tra loro della quantità d; esse sono soggette alla forza F il cui valore è fornito dalla legge di Coulomb:
F= ±(1/4.π.ε).q1.q/d2.
La costante 1/4.π.ε dipende dal mezzo in cui sono immerse le cariche ed ε rappresenta la costante dielettrica assoluta del mezzo o permeattività; di
solito nelle tabelle viene indicata non la costante dielettrica assoluta ma quella relativa con riferimento al vuoto; in tal modo per ottenere la costante dielettrica assoluta del mezzo occorre
moltiplicare la sua costante relativa per la costante assoluta del vuoto ε0 pari a 8,8582.10-12 Farad/m e cioè:
ε=εr.ε0 .
Si definisce campo elettrico E di una carica Q la parte di spazio entro cui si sente l'influenza, mediante una carica unitaria q di un coulomb, della carica Q stessa.
Possiamo allora scrivere relativamente al campo elettrico E :
E=F/q.
Sostituendo ad F il valore fornito dalla legge di coulomb possiamo scrivere: E=Q.q/4.π.ε.d2.q = Q/4.π.ε.d2
V/m
La densità di energia elettrica in un punto è :
WE= 1/2(ε0E2); si misura in J/m3

Nella fig.3a (N) sono indicate le linee di forza del campo elettrico creato da una carica negativa.
Nella fig.3a (P) sono indicate le linee di forza del campo elettrico creato da una carica positiva.
Capacità
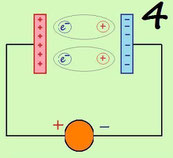
Prendiamo in esame un circuito costituito da un generatore e da due armature collegate con due reofori ai suoi poli come indicatoin fig.4. Le due armature si caricheranno
ed il dielettrico si polarizzerà.
la polarizzazione consiste nella deformazione delle orbite degli elettroni del dielettrico che si allungheranno verso la piastra positiva; analogamente i nuclei degli atomi del dielettrico si
sposteranno verso la piastra negativa.
Se la differenza di potenziale è troppo elevata il campo elettrico diventa tale che gli elettroni si staccano dalle loro orbite ed il dielettrico perde le sue proprietà isolanti (perforazione del
dielettrico).
Il valore limite della differenza di potenziale si chiama rigidità dielettrica e si misura in KV/cm; Esso rappresenta la differenza di potenziale che
una lastra di dielettrico dello spessore di un cm può sopportare senza perdere le sue proprietà isolanti.
La carica q posseduta dalle due armature è proporzionale alla d.d.p. v che vi è fra esse; possiamo pertanto scrivere:
q=Cv dove C rappresenta la capacità del condensatore e si misura in Farad ;
Possiamo inoltre scrivere:
dq=Cdv; ricordando che I=dq/dt; risulta Idt=Cdv ; C=Idt/dv; I=Cdv/dt.
Un condensatore ideale corrisponde ad una capacità perfetta nella quale la corrente è sfasata in ritardo di π/2 rispetto alla tensione.
In realtà però un condensatore perfetto non esiste.

In un condensatore reale infatti esistono varie cause di perdita di energia che risiedono principalmente:
- nel materiale dielettrico sottoposto al campo elettrico, se utilizzato per aumentare la capacità, (La Rrd è una resistenza che sottoposta ad una medesima tensione istantanea v del condensatore , assorbe in ogni istante una energia uguale a quella in realtà assorbita dal materiale dielettrico);
- nella resistenza ohmica del condensatore Rrp da considerare in parallelo con esso;
- nella resistenza delle armature Rrs da considerare invece in serie come indicato in fig.5.
C'è da porre in evidenza che il condensatore reale di fig.5 può essere visto in uno dei due modi riportati in fig.6 cioè può essere rappresentata da un circuito equivalente costituito da una capacità ideale e da una resistenza in serie oppure da una capacità ideale e da una resistenza in parallelo.

Prendiamo in esame i circuiti equivalenti serie e parallelo e per essi tracciamo i diagrammi di fig.7.
In tali diagrammi è stata determinata la corrente I per il circuito equivalente parallelo e la tensione V per il circuito equivalente serie.
Dall'analisi dei grafici si possono determinare i seguenti valori:
δ= tgδ=1/Rp.ω.C = ω.C.Rs;
tgφ = ω.C.Rp = 1/Rs.ω.C,
dove δ, molto piccolo e quindi confondibile con la sua tangente, è l'angolo di perdita e φ
è lo sfasamento fra corrente e tensione.

δ rappresenta le perdite del condensatore per limitare le quali occorre disporre di un buon dielettrico; i
condensatori privi di dielettrico sono chiamati condensatori ad aria.
Anche per i condensatori ad aria comunque il dielettrico non può mancare ed è quello relativo al materiale isolante necessario a fissare le armature; esso fa sentire la propria influenza alle
basse capacità.

La capacità di un condensatore è direttamente proporzionale alla superficie di ciascuna delle due armature affacciate ed inversamente proporzionale alla loro distanza; cioè (vedi fig.8):
C= ε S/d.;
ε e la costante dielettrica del materiale (dielettrico) interposto fra le armature ed è come già visto
ε = εrε0 .
L'energia immagazzinata da un condensatore è: E= 1/2(V2C); questa energia corrisponde al lavoro necessario per portare una carica q da una piastra all'altra sotto un potenziale V, cioè E=L= ∫Vdq ; ora poichè V=q/C possiamo scrivere:
E=∫q/C dq = 1/2(q2/C) =1/2(V2C).
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta


